If A² – A + I = 0, then the inverse of A is

• A + I

• A

• A – I

• A – I

12.

If a² + b² + c² = -2 and  then f(x) is a polynomial of degree

• 1

• 0

• 2

• 2

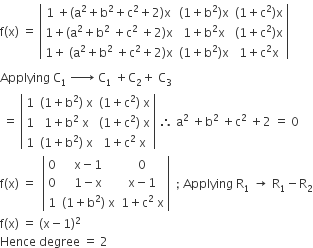
Let A  The only correct statement about the matrix A is

• A is a zero matrix

• A² = I

• A⁻¹ does not exist

• A⁻¹ does not exist

Let .If B is the inverse of matrix A, then α is

• -2

• 5

• -2

• -2

The linear system of equations

$$\begin{gathered} \left\{8\mathrm{x} - 3\mathrm{y} - 5\mathrm{z} = 0 \\ 5\mathrm{x} - 8\mathrm{y} + 3\mathrm{z} = 0 \\ 3\mathrm{x} + 5\mathrm{y} - 8\mathrm{z} = 0\right\} \end{gathered}$$

has

• Only zero solution

• Only finite number of non-zero solution

• No non-zero solution

• Infinitely many non-zero solution

Let P be the set of non-singular matrices of order 3 over R and Q be the set of all orthogonal of matrices of order 3 over R. Then,

• P is proper subset of Q

• Q is proper subset of P

• Neither P is proper subset of Q nor Q is proper subset of P

• $\mathrm{P} \cap \mathrm{Q} = \mathrm{\varphi }$, the void set

Let A = $\left(\begin{array}{ccc}1& 1& 1\\ 0& 1& 1\\ 0& 0& 1\end{array}\right)$. Then, for positive integer n, Aⁿ is

• $\left(\begin{array}{ccc}1& \mathrm{n}& {\mathrm{n}}^2\\ 0& {\mathrm{n}}^2& \mathrm{n}\\ 0& 0& \mathrm{n}\end{array}\right)$

• $\left(\begin{array}{ccc}1& \mathrm{n}& \mathrm{n}\left(\frac{\mathrm{n} + 1}{2}\right)\\ 0& 1& \mathrm{n}\\ 0& 0& 1\end{array}\right)$

• $\left(\begin{array}{ccc}1& {\mathrm{n}}^2& \mathrm{n}\\ 0& \mathrm{n}& {\mathrm{n}}^2\\ 0& 0& {\mathrm{n}}^2\end{array}\right)$

• $\left(\begin{array}{ccc}1& \mathrm{n}& 2\mathrm{n} - 1\\ 0& \frac{\mathrm{n} + 1}{2}& {\mathrm{n}}^2\\ 0& 0& \frac{\mathrm{n} + 1}{2}\end{array}\right)$

Let a, b, c be such that b(a + c) $\ne$ 0.

If $\left|\begin{array}{ccc}\mathrm{a}& \mathrm{a} +\hspace{0.17em}1& \mathrm{a} - 1\\ - \mathrm{b}& \mathrm{b} +\hspace{0.17em}1& \mathrm{b} - 1\\ \mathrm{c}& \mathrm{c} - 1& \mathrm{c} +\hspace{0.17em} 1\end{array}\right| + \left|\begin{array}{ccc}\mathrm{a} + 1& \mathrm{b} + 1& \mathrm{c} - 1\\ \mathrm{a} - 1& \mathrm{b} - 1& \mathrm{c} + 1\\ (- 1{)}^{\mathrm{n} + 2}\mathrm{a}& (- 1{)}^{\mathrm{n} + 2}\mathrm{b}& (- 1{)}^{\mathrm{n}}\mathrm{c}\end{array}\right|$ = 0, then the value of n is 

• any integer

• zero

• any even integer

• any odd integer

If x, y and z are greater than 1, then the value of

$\left|\begin{array}{ccc}1& {\log }_{\mathrm{x}}\left(\mathrm{y}\right)& {\log }_{\mathrm{x}}\left(\mathrm{z}\right)\\ {\log }_{\mathrm{y}}\left(\mathrm{x}\right)& 1& {\log }_{\mathrm{y}}\left(\mathrm{z}\right)\\ {\log }_{\mathrm{z}}\left(\mathrm{x}\right)& {\log }_{\mathrm{z}}\left(\mathrm{y}\right)& 1\end{array}\right|$ is

• $\log \left(\mathrm{x}\right) . \log \left(\mathrm{y}\right) . \log \left(\mathrm{z}\right)$

• $\log \left(\mathrm{x}\right) + \log \left(\mathrm{y}\right) + \log \left(\mathrm{z}\right)$

• 0

• $1 - \left\{\left(\log \left(\mathrm{x}\right)\right) . \log \left(\mathrm{y}\right) . \log \left(\mathrm{z}\right)\right\}$

Let A be a 3 x 3 matrix and B be its adjoint matrix. If I $\left|\mathrm{B}\right|$ = 64, then $\left|\mathrm{A}\right|$ is equal to

• $\pm 2$

• $\pm 4$

• $\pm 8$

• $\pm 12$