 Multiple Choice Questions
Multiple Choice QuestionsIf a straight line perpendicular to 2x - 3y + 7 = 0 forma triangle with the co-ordinate axes whose area is 3 sq. units, then the equation of the straight line is
If ( - 2, 6) is the image of the point (4, 2) with respect to the line L = 0, then L is equal to
6x - 4y - 7 = 0
2x + 3y - 5 = 0
3x - 2y + 5 = 0
3x - 2y + 10 = 0
If the co-ordinate axes are the bisectors of the angles between the pair of lines
a + b = 0
h = 0
If the lines 4x + 3y - 1 = 0, x - y + 5 = 0 and kx + 5y - 3 are concurrent, then k is equal to
4
5
6
7
If the pair of straight lines given by Ax2 + 2Hxy + By2 = 0 (H2 > AB) forms an equilateral triangle with line ax + by + c = 0, then (A + 3B)(3A + B) is equal to :
H2
- H2
2H2
4H2
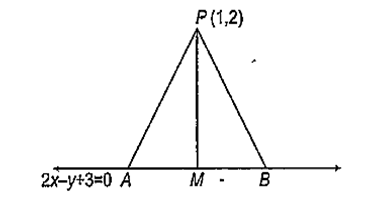
Suppose A, B are two points on 2x - y + 3 = 0 and P (1, 2) is such that PA = PB. Then, the mid-point of AB is
A.
Area of the triangle formed by the lines 3x2 + 4xy + y2 = 0, 2x - y = 6 is
16 sq. units
25 sq. units
36 sq. units
49 sq. units
