If from a point P (a, b, c) perpendiculars PA, PB are drawn to yz and zx planes, then the equation of the plane OAB is

• bcx + cay + abz = 0

• bcx + cay - abz = 0

• bcx - cay + abz = 0

• - bcx + cay + abz = 0

If P (x, y, z) is a point on the line segment joning Q (2, 2, 4) and R (3, 5, 6) such thatprojections of OP on the axes are $\frac{13}{5}, \frac{19}{5}, \frac{26}{5}$ respectively, then P divides QR in the ratio

• 1 : 2

• 3 : 2

• 2 : 3

• 1 : 3

The equation to the plane through the points (2, 3, 1) and ( 4, - 5 3) paralled to x - axis is

• x + y + 4z = 7

• x + 4z = 7

• y - 4z = 7

• y + 4z = 7

The angle between r = (1 + 2µ)i +(2 + µ)j + (2µ - 1)k and the plane 3x - 2y + 6z = 0 (whereµ is a scalar) is

• ${\sin }^{-1}\left(\frac{15}{21}\right)$

• ${\cos }^{-1}\left(\frac{16}{21}\right)$

• ${\sin }^{-1}\left(\frac{16}{21}\right)$

• $\frac{\mathrm{\pi }}{2}$

The length of the shortest distance between the two lines r = (- 3i + 6j) + s (- 4i + 3j + 2k) and r = (- 2i + 7k) + t(- 4i + j + k) is

• 7 unit

• 13 unit

• 8 unit

• 9 unit

The perpendicular distance of the point (6, 5, 8) from y-axis is

• 5 unit

• 6 unit

• 8 unit

• 10 unit

The equation of the plane passing through the origin and containing the line

$\frac{\mathrm{x} - 1}{5} = \frac{\mathrm{y} - 2}{4} = \frac{\mathrm{z} - 3}{5}$ is

• x + 5y - 3z = 0

• x - 5y + 3z = 0

• x - 5y - 3z = 0

• 3x - 10y + 5z = 0

98.

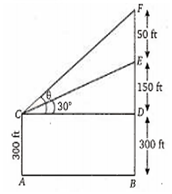
A flagpole stands on a building of height 450 ft and an observer on a level ground is 300 ft from the base of the building. The angle of elevation of the bottom of the flagpole is 30° and the height of the flagpole is SO ft. If 8 is the angle of elevation of the top of the flagpole, then tan$\left(\mathrm{\theta }\right)$ is equal to

• $\frac{4}{3\sqrt{3}}$

• $\frac{\sqrt{3}}{2}$

• $\frac{9}{2}$

• $\frac{\sqrt{3}}{5}$

If A (0, 0), B (12, 0), C (12, 2), D (6, 7) and E (0, 5) are the vertices of the pentagon ABCDE, then its area in square units, is

• 58

• 60

• 61

• 63

The equation of the plane perpendicular to the line $\frac{\mathrm{x} - 1}{1} = \frac{\mathrm{y} - 2}{- 1} = \frac{\mathrm{z} + 1}{2}$  afd passing through the point (2, 3, 1) is

• $\overrightarrow{\mathrm{r}} . \left(\hat{\mathrm{i}} + \hat{\mathrm{j}} + 2\hat{\mathrm{k}}\right) = 1$

• $\overrightarrow{\mathrm{r}} . \left(\hat{\mathrm{i}} - \hat{\mathrm{j}} + 2\hat{\mathrm{k}}\right) = 1$

• $\overrightarrow{\mathrm{r}} . \left(\hat{\mathrm{i}} - \hat{\mathrm{j}} + 2\hat{\mathrm{k}}\right) = 7$

• $\overrightarrow{\mathrm{r}} . \left(\hat{\mathrm{i}} + \hat{\mathrm{j}} - 2\hat{\mathrm{k}}\right) = 10$