 Multiple Choice Questions
Multiple Choice QuestionsThe ratio in which the line joining (2, 4, 5), (3, 5, - 4) is divided by the yz-plane is
2 : 3
3 : 2
- 2 : 3
4 : - 3
The equation of line of intersection of planes 4x + 4y - 5z = 12, 8x + 12y - 13z = 32can be written as :
The equation of the plane, which makes with co-ordinate axes, a triangle with its centroid is :
A variable plane moves so that sum of the reciprocals of its intercepts on the co-ordinate axes is 1/2. Then the plane passes through :
(- 1, 1, 1)
(2, 2, 2)
(0, 0, 0)
The direction cosines l, m, n of two lines are connected by the relations l + m + n = 0, lm = 0, then the angle between them is :
0
Cosine of the angle between two diagonals of a cube is equal to :
None of these
B.
Let OA, OB, OC be the sides of a cube such that OA = OB = OC = a
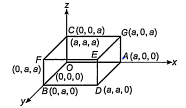
Co-ordinate of the vertices of cube are O(0, 0, 0), A(a, 0, 0), B(0, a, 0), C(0, 0, a), D(a, a, 0), E(a, a, a), F(0, a, a) and G(a, 0, a).
Direction ratios of OE are (a - 0, a - 0, a - 0) i.e., (a, a, a).
The equation of the bisector of the acute angles between the lines 3x - 4y + 7=0 and 12x + 5y - 2 = 0 is :
99x - 27y - 81 = 0
11x - 3y + 9 = 0
21x + 77y - 101 = 0
21x + 77y + 101 = 0
