 Multiple Choice Questions
Multiple Choice QuestionsEquation of line passing through the point (2, 3, 1) and parallel to the line of intersection of the planes x - 2y - z + 5 = 0 and x + y + 3z = 6 is
Foot of perpendicular drawn from the origin to the plane 2x - 3y + 4z = 29 is
(7, - 1, 3)
(5, - 1, 4)
(5, - 2, 3)
(2, - 3, 4)
The vector equation of the plane, which is at a distance of , from the origin and the normal from the origin is is
Find the coordinates of the foot of the perpendicular drawn from the origin to the plane 5y + 8 = 0.
The perpendicular distance of the point P(6, 7, 8) from XY-plane is
6
7
5
8
D.
8
Accordmg to the question
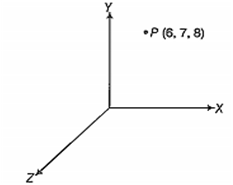
Distance of any point from XY - plane is =
=
