A class has fifteen boys and five girls.Suppose three students are selected at random from the class. The probability that there are two boys and one girl is

• $\frac{35}{76}$

• $\frac{35}{38}$

• $\frac{7}{76}$

• $\frac{35}{72}$

$\mathrm{a} = \mathrm{i} + \mathrm{j} - 2\mathrm{k} \Rightarrow \sum _{}{\left\{\left(\mathrm{a} \times \mathrm{i}\right) \times \mathrm{j}\right\}}^2 = ?$

• $\sqrt{6}$

• 6

• 36

• $6\sqrt{6}$

Let a, b and c be three non-coplanar vectors and let p, q and r be the vectors defined by

$$\begin{gathered} \mathrm{p} = \frac{\mathrm{b} \times \mathrm{c}}{\left[\begin{array}{ccc}\mathrm{a}& \mathrm{b}& \mathrm{c}\end{array}\right]}, \mathrm{q} = \frac{\mathrm{c} \times \mathrm{a}}{\left[\begin{array}{ccc}\mathrm{a}& \mathrm{b}& \mathrm{c}\end{array}\right]}, \mathrm{r} = \frac{\mathrm{a} \times \mathrm{b}}{\left[\mathrm{abc}\right]} \mathrm{Then}, \\ \left(\mathrm{a} + \mathrm{b}\right) . \mathrm{p} + \left(\mathrm{b} + \mathrm{c}\right) . \mathrm{q} + \left(\mathrm{c} + \mathrm{a}\right) . \mathrm{r} = ? \end{gathered}$$

• 0

• 1

• 2

• 3

Let a = i + 2j + k, b = i - j + k, c = i + j - k.

A vector in the plane of a and b has projection $\frac{1}{\sqrt{3}}$ on c. Then, one such vector is

• 4i + j - 4k

• $3\mathrm{i} + \mathrm{j} - 3\mathrm{k}$

• 4i - j + 4k

• 2i + j + 2k

The point if intersection of the lines

l₁ : r(t) = (i - 6j + 2k) + t(i + 2j + k)

l₂ : R(u) = (4j + k) + u(2i + j + 2k) is

• (10, 12, 11)

• (4, 4, 5)

• (6, 4, 7)

• (8, 8, 9)

456.

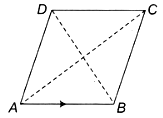
The vectors AB = 3i - 2j + 2k and BC = i - 2k are the adjacent sides of a parallelogram. The angle between its diagonals is

• $\frac{\mathrm{\pi }}{2}$

• $\frac{\mathrm{\pi }}{3} \mathrm{or} \frac{2\mathrm{\pi }}{3}$

• $\frac{3\mathrm{\pi }}{4} \mathrm{or} \frac{\mathrm{\pi }}{4}$

• None of these

The points whose position vectors are 2i + 3j + 4k, 3i + 4j + 2k and 4i + 2j + 3k are the vertices of

• an isosceles triangle

• Right angled triangle

• Equilateral triangle

• Right angled isosceles triangle

P, Q, R and S are four pots with the position vectors 3i - 4j + 5k, - 4i + 5j + k and - 3i + 4j + 3k respectively. Then, the line PQ meets the line RS at the point

• 3i + 4j + 3k

• - 3i + 4j + 3k

• - i + 4j + k

• i + j + k

$\mathrm{If} \mathrm{a} \ne 0, \mathrm{b} \ne 0, \mathrm{c} \ne 0, \mathrm{a} \times \mathrm{b} = 0 \mathrm{and} \mathrm{b} \times \mathrm{c} = 0, \mathrm{then} \mathrm{a} \times \mathrm{c} = ?$

• b

• a

• 0

• i + j + k

The shortest distance between r = 3i + 5j + 7k + λ(i + 2j + k) and r = - i - j - k + μ(7i - 6j + k) is

• $\frac{16}{5\sqrt{5}}$

• $\frac{26}{5\sqrt{5}}$

• $\frac{36}{5\sqrt{5}}$

• $\frac{46}{5\sqrt{5}}$