 Multiple Choice Questions
Multiple Choice QuestionsWhat is the dimensions of a magnetic field B in terms of C ( = coulomb ), M, L, T?
[ M1 L-1 T-2 C ]
[ M1 L0 T-1 C-1 ]
[ M1 L0 T-2 C ]
[ M1 L0 T-1 C ]
When a positively charged particle enters into a uniform magnetic field with uniform velocity, its trajectory can be
(i) a straight line (ii) a circle (iii) a helix
(i) only
(i) or (ii)
(i) or (iii)
any one of (i), (ii) and (iii)
Assertion: Magnetic field lines are continuous and closed.
Reason: Magnetic monopole does not exist.
If both assertion and reason are true but reason is not the correct explanation of assertion.
If both assertion and reason are true but reason is not the correct explanation of assertion.
If assertion is true but reason is false.
If both assertion and reason are false.
Assertion: Magnetic force between two short magnets, when they are co-axial follows inverse square law of distance.
Reason: The magnetic forces between two poles do not follow inverse square law of distance.
If both assertion and reason are true and reaon is correct explanation of assertion.
If both assertion and reason are true and reaon is not the correct explanation of assertion.
If assertion is true but reason is false.
If both assertion and reason are false.
Assertion: If a proton and an a-particle enter a uniform magnetic field perpendicularly with the same speed, the time period of revolution of a particle is double that of proton.
Reason: In a magnetic field, the period of revolution of a charged particle is directly proportional to the mass of the particle and is inversely proportional to charge of particle.
If both assertion and reason are true and reason is the correct explanation of assertion
If both assertion and reason are true but reason is not the correct explanation of assertion
If assertion is true but reason is false
If both assertion and reason are false.
A moving coil galvanometer has a resistance of 900 Ω. In order to send only 10 % of the main current through this galvanometer, the resistance of the required shunt is
0.9 Ω
100 Ω
405 Ω
90 Ω
The intensity of magnetic field due to an isolated pole of strength mp at a point distant r from it will be
mp/r2
mp r2
r2/ mp
mp/r
The ratio of magnetic fields on the axis of a circular current carrying coil of radius a to the magnetic field at its centre will be
A.
Consider a circular radius of a, carrying a current I. Consider a point P, which is at a distance x from the centre of coil. We can consider that the loop is made p of a large number of short element, generating small magnetic fields. So the total field at P will be the sum of the contributions of all these elements. At the centre of coil, the field will be uniform.
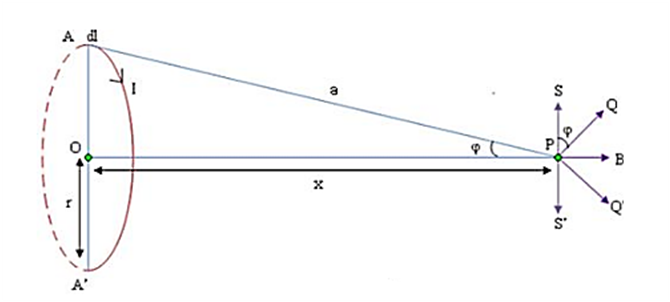
By Biot- Savart’s law, the field dB due to a small element dl of the circle, centered at A is given by
dB =
This can be resolved into two components, one along the axis OP, and other PS, which is perpendicular to OP. PS is exactly cancelled by the perpendicular component PS’ of the field due to a current and centered at A’. So, the total magnetic field at a point which is at a distance x away from the axis of a circular coil of radius a is given by,
dB =
μ0, I are constants and by divide and multiply by a2 on denominator and numerator we get
dB =
