A current loop in a magnetic field

• experiences a torque whether the field is uniform or non- uniform in all orientations

• can be in equilibrium in one orientations

• can be equilibrium in two orientations, both the equilibrium states are unstable

• can be in equilibrium in two orientations, one stable while the other is unstable

A bar magnet of length l and magnetic dipole moment M is bent in the form of an arc as shown in figure. The new magnetic dipole moment will be

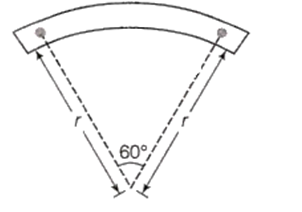
• M

• $\frac{3}{\mathrm{\pi }} \mathrm{M}$

• $\frac{2}{\mathrm{\pi }} \mathrm{M}$

• $\frac{\mathrm{M}}{2}$

343.

A galvanometer having internal resistance 10 Ω requires 0.01 A for a full scale deflection. To convert this galvanometer to a voltmeter of full-scale deflection at 120 V, we need to connect a resistance of

• 11990 Ω in series

• 11990 Ω in parallel

• 12010 Ω in series

• 12010 Ω in parallel

An electron in a circular orbit ofradius 0.05 nm performs 10¹⁶ revolutions per second. The magnetic moment due to this rotation of electron is (in Am²)

• 2.16 × 10^-23

• 3.21 × 10^-22

• 3.21 × 10^-24

• 1.26 × 10^-23

A very small circular loop of radius a is initially (at t = 0) coplanar and concentric with a much larger fixed circular loop of radius b. A constant current I flows in the larger loop. The smaller loop is rotated with a constant angular speed ω about the common diameter. The emf induced in the smaller loop as a function of time t is

• $\frac{{\mathrm{\pi a}}^2{\mathrm{\mu }}_0\mathrm{I}}{2\mathrm{b}} \mathrm{\omega } \cos \left(\mathrm{\omega t}\right)$

• $\frac{{\mathrm{\pi a}}^2{\mathrm{\mu }}_0\mathrm{I}}{2\mathrm{b}} \mathrm{\omega } \sin \left({\mathrm{\omega }}^2{\mathrm{t}}^2\right)$

• $\frac{{\mathrm{\pi a}}^2{\mathrm{\mu }}_0\mathrm{I}}{2\mathrm{b}} \mathrm{\omega } \sin \left(\mathrm{\omega t}\right)$

• $\frac{{\mathrm{\pi a}}^2{\mathrm{\mu }}_0\mathrm{I}}{2\mathrm{b}} \mathrm{\omega } {\sin }^2 \left(\mathrm{\omega t}\right)$

A proton of mass m and charge q is moving in a plane with kinetic energy E. If there exists a uniform magnetic field B, perpendicular to the plane of the motion, the proton will move in a circular path of radius

• $\frac{2\mathrm{Em}}{\mathrm{qB}}$

• $\frac{\sqrt{2\mathrm{Em}}}{\mathrm{qB}}$

• $\frac{\sqrt{\mathrm{Em}}}{2\mathrm{qB}}$

• $\sqrt{\frac{2\mathrm{Eq}}{\mathrm{mB}}}$

A long conducting wire carrying a current I is bent at 120° (see figure). The magnetic field B at a point P on the right bisector of bending angle at a distance d from the bend is (µ₀ is the permeability of free space)

• $\frac{3{\mathrm{\mu }}_0\mathrm{I}}{2\mathrm{\pi d}}$

• $\frac{{\mathrm{\mu }}_0\mathrm{I}}{2\mathrm{\pi d}}$

• $\frac{{\mathrm{\mu }}_0\mathrm{I}}{\sqrt{3} \mathrm{\pi d}}$

• $\frac{\sqrt{3} {\mathrm{\mu }}_0\mathrm{I}}{2 \mathrm{\pi d}}$

A stream of electrons and protons are directed towards a narrow slit in a screen (see figure). The intervening region has a uniform electric field E (vertically downwards) and a uniform magnetic field B (out of the plane of the figure) as shown. Then

• electrons and protons with speed $\frac{\left|\mathrm{E}\right|}{\left|\mathrm{B}\right|}$ will pass through the slit

• protons with speed $\frac{\left|\mathrm{E}\right|}{\left|\mathrm{B}\right|}$ will pass through the slit, electron of the same speed will not

• neither electrons nor protons will go through the slit irrespective of their speed

• electrons will always be deflected upwards irrespective of their speed

Two particles, A and B, having equal charges, after being accelerated through the same potential difference enter into a region of uniform magnetic field and the particles describe circular paths of radii R₁ and R₂, respectively. The ratio of the masses of A and B is

• $\sqrt{{\mathrm{R}}_1/{\mathrm{R}}_2}$

• R₁ / R₂

• (R₁ / R₂)²

• (R₂ / R₁)²

A straight conductor 0.1 m long moves in a uniform magnetic field 0.1 T. The velocity of the conductor is 15 m/s and is directed perpendicular to the field. The emf induced between the two ends of the conductor is

• 0.10 V

• 0.15 V

• 1.50 V

• 15.00 V