The speed of light in the medium is

•  maximum on the axis of the beam

• minimum on the axis of the beam

• the same everywhere in the beam

• the same everywhere in the beam

An initially parallel cylindrical beam travels in a medium of refractive index μ(I) = μ₀ +μ₂I , where μ₀ and μ₂ are positive constants and I is the intensity of the light beam. The intensity of the beam is decreasing with increasing radius. 

As the beam enters the medium, it will

• travel as a cylindrical beam

• diverge

• converge

• converge

An initially parallel cylindrical beam travels in a medium of refractive index μ(I) = μ0 +μ2I , where μ0 and μ2 are positive constants and I is the intensity of the light beam. The intensity of the beam is decreasing with increasing radius.
The initial shape of the wavefront of the beam is

• convex

• concave

• convex near the axis and concave near the periphery

• convex near the axis and concave near the periphery

A mixture of light, consisting of wavelength 590 nm and an unknown wavelength, illuminates Young's double slit and gives rise to two overlapping interference patterns on the screen. The central maximum of both lights coincide. Further, it is observed that the third bright fringe of known light coincides with the 4th bright fringe of the unknown light. From this data, the wavelength of the unknown light is

• 393.4 nm

• 885.0 nm

• 442.5 nm

• 442.5 nm

Young’s double slit experiment the intensity at a point where the path-difference is λ/6(λ being the wavelength of the light used) is I. If I₀ denotes the maximum intensity, I/I₀ is equal to

• 
• 

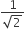
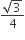
• 1/2

• 1/2

The refractive index of glass is 1.520 for red light and 1.525 for blue light. Let D₁ and D₂ be an of minimum deviation for red and blue light respectively in a prism of this glass. Then

• D₁ > D₂

• D₁ < D₂

• D₁ = D₂

• D₁ = D₂

17.

A Young’s double slit experiment uses a monochromatic source. The shape of the interference fringes formed on a screen is

• hyperbola

• circle

• straight line

• straight line

A fish looking up through the water sees the outside world contained in a circular horizon. If the refractive index of water is 4/3 and the fish is 12 cm below the surface, the radius of this circle in cm is

Two point white dots are 1 mm apart on a black paper. They are viewed by eye of pupil diameter 3 mm. Approximately, what is the maximum distance at which these dots can be resolved by the eye? [ Take wavelength of light = 500 nm ]

• 5 m

• 1 m

• 6 m

• 6 m

A thin glass (refractive index 1.5) lens has an optical power of – 5D in air. Its optical power in a liquid medium with refractive index 1.6 will be

• 1 D

• 5/8 D

• -1 D

• -1 D