 Multiple Choice Questions
Multiple Choice QuestionsIf increases in the interval T and decreases in the interval S, then which one of the following is correct ?
Consider the function
f(x) = 3x4 – 20x3 – 12x2 + 288x + 1
In which one of the following intervals is the function decreasing ?
( - 2, 3)
(3, 4)
(4, 6)
No
Consider the function
f(x) = 3x4 – 20x3 – 12x2 + 288x + 1
In which one of the following intervals is the function increasing ?
( - 2, 3)
(3, 4)
(4, 6)
(6, 9)
Let l be the length and b be the breadth of a rectangle such that l x b = k. What is the maximum area of the rectangle ?
2k2
k2
D.
Here ABCD is rectangle which have
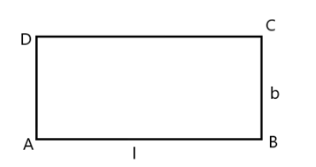
Length AB = l and breadth BC = b
Let area is y
l + b = k
l = k - b (given)
Now, area y = lb = l(k - l) = kl - l2
For maximum area y,
The radius of a circle is increasing at the rate of 0.7 cm/sec. What is the rate of increase of its circumference ?
4.4 cm/sec
8.4 cm/sec
8.8 cm/sec
15.4 cm/sec
