Let asin²(x) + bcos²(x) = c; bsin²(y) + acos²(y) = d and p tan(x) = qtan(y).

What is tan²(x) equal to ?

• $\frac{\mathrm{c} - \mathrm{b}}{\mathrm{a} - \mathrm{c}}$

• $\frac{\mathrm{a} - \mathrm{c}}{\mathrm{c} - \mathrm{b}}$

• $\frac{\mathrm{c} - \mathrm{a}}{\mathrm{c} - \mathrm{b}}$

• $\frac{\mathrm{c} - \mathrm{b}}{\mathrm{c} - \mathrm{a}}$

Consider the following statements :

1) If in a triangle ABC, A = 2B and b = c, then it must be an obtuse-angled triangle.

2) There exists no triangle ABC with A = 40^o. B = 65^o and $\frac{\mathrm{a}}{\mathrm{c}} = \sin \left(40°\right)\csc \left(15°\right)$

Which of the above statements is/are correct ?

• 1 only

• 2 only

• Both 1 and 2

• Neither 1 nor 2

What is the value of $\cos \left(48°\right) - \cos \left(12°\right) ?$

• $\frac{\sqrt{5} - 1}{4}$

• $\frac{1 - \sqrt{5}}{4}$

• $\frac{\sqrt{5} + 1}{2}$

• $\frac{1 - \sqrt{5}}{8}$

Consider the following statements :

1) If ABC is a right-angled triangle, right-angled at A and if then cosec(C) = 3

2) If bcos(B) = ccos(C) and if the triangle ABC is not right-angled, then ABC must be isosceles.

Which of the above statements is/are correct ?

• 1 only

• 2 only

• Both 1 and 2

• Neither 1 nor 2

What is the value of $8\cos \left(10°\right) . \cos \left(20°\right) . \cos \left(40°\right) ?$

• $\tan \left(10°\right)$

• $\cot \left(10°\right)$

• $\csc \left(10°\right)$

• $\sec \left(10°\right)$

What is sin(3x) + cos(3x) + 4sin(3x) – 3sin(x) + 3cos(x) – 4cos(3x) equal to ?

• 0

• 1

• 2sin(2x)

• 4cos(4x)

A and B are positive acute angles such that cos(2B) = 3 sin(2A) and 3sin(2A) = 2sin(2B). What is the value of (A + 2B) ?

• $\frac{\mathrm{\pi }}{6}$

• $\frac{\mathrm{\pi }}{4}$

• $\frac{\mathrm{\pi }}{3}$

• $\frac{\mathrm{\pi }}{2}$

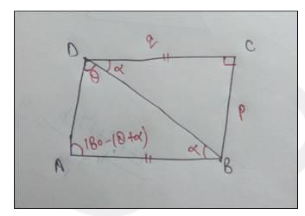
ABC is a trapezium such that AB and CD are parallel and BC is perpendicular to them. Let ∠ADB = θ, ∠ABD = α, BC = p and CD = q.

$\mathrm{If} \tan \left(\mathrm{\theta }\right) = \frac{\cos \left(17°\right) - \sin \left(17°\right)}{\cos \left(17°\right) + \sin \left(17°\right)}$ then what is the value of θ ?

• $0°$

• $28°$

• $38°$

• 52$°$

ABC is a trapezium such that AB and CD are parallel and BC is perpendicular to them. Let ∠ADB = θ, ∠ABD = α, BC = p and CD = q.

What is AB equal to ?

• $\frac{\left({\mathrm{p}}^2 - {\mathrm{q}}^2\right)\sin \left(\mathrm{\theta }\right)}{\mathrm{pcos}\left(\mathrm{\theta }\right) + \mathrm{qsin}\left(\mathrm{\theta }\right)}$

• $\frac{\left({\mathrm{p}}^2 - {\mathrm{q}}^2\right)\cos \left(\mathrm{\theta }\right)}{\mathrm{pcos}\left(\mathrm{\theta }\right) + \mathrm{qsin}\left(\mathrm{\theta }\right)}$

• $\frac{\left({\mathrm{p}}^2 + {\mathrm{q}}^2\right)\sin \left(\mathrm{\theta }\right)}{\mathrm{pcos}\left(\mathrm{\theta }\right) + \mathrm{qsin}\left(\mathrm{\theta }\right)}$

• $\frac{\left({\mathrm{p}}^2 - {\mathrm{q}}^2\right)\cos \left(\mathrm{\theta }\right)}{\mathrm{qcos}\left(\mathrm{\theta }\right) + \mathrm{psin}\left(\mathrm{\theta }\right)}$

100.

ABC is a trapezium such that AB and CD are parallel and BC is perpendicular to them. Let ∠ADB = θ, ∠ABD = α, BC = p and CD = q.

Consider the following :

1) ADsin(θ) = ABsin(α)

2) BDsin(θ) = ABsin(θ + α)

Which of the above is/are correct ?

• 1 only

• 2 only

• Both 1 and 2

• Neither 1 nor 2