Three resistances 2 Ω, 3 Ω and 4 Ω are connected in parallel. The ratio of currents passing through them when a potential difference is applied across its ends will be

• 5 : 4 : 3

• 6 : 3 : 2

• 4 : 3 : 2

• 6 : 4 : 3

Four identical cells of emf E and internal resistance r are to be connected in series. Suppose, if one of the cell is connected wrongly, the equivalent emf and effective internal resistance of the combination is

• 2E and 4r

• 4E and 4r

• 2E and 2r

• 4E and 2r

In the circuit shown below, the ammeter and the voltmeter readings are 3A and 6V respectively. Then, the value of the resistance R is

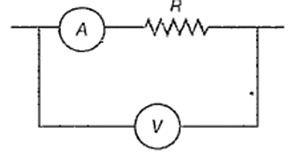
• < 2 Ω

• 2 Ω

• ≥ 2 Ω

• > 2 Ω

Two cells of emf E₁ and E₂ are joined in opposition (such that E₁ > E₂). If r₁ and r₂ be the internal resistances and R be the external resistance, then the terminal potential difference is

• $\frac{{\mathrm{E}}_1 - {\mathrm{E}}_2}{{\mathrm{r}}_1 + {\mathrm{r}}_2} \times \mathrm{R}$

• $\frac{{\mathrm{E}}_1 + {\mathrm{E}}_2}{{\mathrm{r}}_1 + {\mathrm{r}}_2} \times \mathrm{R}$

• $\frac{{\mathrm{E}}_1 - {\mathrm{E}}_2}{{\mathrm{r}}_1 + {\mathrm{r}}_2 + \mathrm{R}} \times \mathrm{R}$

• $\frac{{\mathrm{E}}_1 + {\mathrm{E}}_2}{{\mathrm{r}}_1 + {\mathrm{r}}_2 + \mathrm{R}} \times \mathrm{R}$

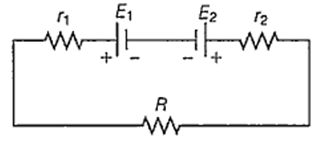
The resistance ofa bulb filament is 100 Ω at a temperature of 100°C. If its temperature coefficient of resistance be 0.005 per°C, then its resistance will become 200 Ω at a temperature

• 500°C

• 300°C

• 200°C

• 400°C

In Wheatstone network, P = 2 Ω, Q = 2 Ω, R = 2 Ω and S = 3 Ω. The resistance with which S is to be shunted in order that the bridge may be balanced is

• 4 Ω

• 1 Ω

• 6 Ω

• 2 Ω

197.

Two parallel wires 1 m apart carry currents of 1 A and 3 A respectively in opposite directions. The force per unit length acting between two wires is

• 6 × 10^-5 Nm^-1 repulsive

• 6 × 10^-7 Nm^-1 repulsive

• 6 × 10^-5 Nm^-1 attractive

• 6 × 10^-7 Nm^-1 attractive

Mobility of free electrons in a conductor is

• directly proportional to electron density

• directly proportional to relaxation time

• inversely proportional to electron density

• inversely proportional to relaxation time

Variation of resistance of the conductor with temperature is as shown

The temperature coefficient (α) of the conductor is

• $\frac{{\mathrm{R}}_0}{\mathrm{m}}$

• mR₀

• m²R₀

• $\frac{\mathrm{m}}{{\mathrm{R}}_0}$

Potential difference between A and B in the following circuit

• 4 V

• 5.6 V

• 2.8 V

• 6 V