A 700 g solid cube having an edge of length 10 cm floats in water. The volume of the cube outside water is :

• 2.4 cm³

• 4.8 cm³

• 300 cm³

• 500 cm³

162.

Consider the following equation of Bernoulli's theorem

$\mathrm{P} + \frac{1}{2}{\mathrm{\rho v}}^2 + \mathrm{\rho gh} = \mathrm{K}$ (constant)

The dimensions of K/P are same as that of which of the following?

• Thrust

• Pressure

• Angle

• Viscosity

Why the dam of the water reservoir is thick at the bottom?

• Quantity of water increases with depth

• Density of water increases with depth

• Pressure of water increases with depth

• Temperature of water increases with depth

When a drop splits up into a number of drops, then :

• Area increases

• Volume increases

• Energy is absorbed

• Energy is liberated

At which of the following temperature, the value of the surface tension of water is minimum?

• 4°C

• 25°C

• 50°C

• 75°C

In a capillary tube experiment, a vertical, 30 cm long capillary tube is dipped in water. The water rises upto a height of 10 cm due to capillary action. If this experiment is conducted in a freely falling elevator, the length of the water column becomes :

• 10 cm

• 20 cm

• 30 cm

• zero

An aeroplane gets its upward lift due to a phenomenon described by the :

• Archimedes principle

• Bernoulli's principle

• Buoyancy principle

• Pascal law

A wooden block is taken to the bottom of a deep, calm lake of water and then released. It rises up with a :

• constant acceleration

• decreasing aceleration

• constant velocity

• decreasing velocity

A hollow conducting sphere is placed in an electric field produced by a point charge placed at P as shown in the figure. Let V_A, V_B, V_C be the potentials at points A, B and C respectively. Then :

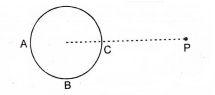
• V_C > V_B

• V_B > V_c

• V_A > V_B

• V_A = V_C

The radius R of the soap bubble is doubled under isothermal condition. If T be the surface tension of soap bubble, the required surface energy in doing so is given by:

• 32πR²T

• 24πR²T

• 8πR²T

• 4πR²T