The period of a simple pendulum inside a stationary lift is T. The lift accelerates upwards with an acceleration of g/3. The time period of pendulum will be

• $\sqrt{2} \mathrm{T}$

• $\frac{\mathrm{T}}{\sqrt{2}}$

• $\frac{\sqrt{3}}{2} \mathrm{T}$

• $\frac{\mathrm{T}}{3}$

The amplitude of- SHM $\mathrm{y} = 2 \left( \sin 5\mathrm{\pi t} + \sqrt{2} \cos \mathrm{\pi t}\right)$ is

• 2

• $2\sqrt{2}$

• 4

• $2\sqrt{3}$

The total energy of a simple harmonic oscillator is proportional to

• square root of displacement

• velocity

• square of the amplitude

• amplitude

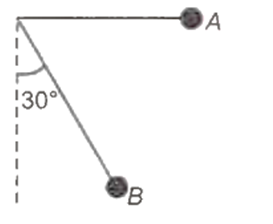
A simple pendulum is released from A as shown. If m and l represent the mass of the bob and length of the pendulum, the gain in kinetic energy at B is

• $\frac{\mathrm{mgl}}{2}$

• $\frac{\mathrm{mgl}}{\sqrt{2}}$

• $\frac{\sqrt{3}}{2} \mathrm{mgl}$

• $\frac{2}{\sqrt{3}} \mathrm{mgl}$

In damped oscillations, the amplitude of oscillations is reduced to one-third of its initial value a₀ at the end of 100 oscillations. When the oscillator completes 200 oscillations, its amplitude must be

• $\frac{{\mathrm{a}}_0}{2}$

• $\frac{{\mathrm{a}}_0}{6}$

• $\frac{{\mathrm{a}}_0}{9}$

• $\frac{{\mathrm{a}}_0}{4}$

A particle executes simple harmonic motion with a time period of 16 s. At time t = 2 s, the particle crosses the mean position while at t = 4s, its velocity is 4 ms^-1. The amplitude of motion in metre is

• $\sqrt{2} \mathrm{\pi }$

• $16\sqrt{2} \mathrm{\pi }$

• $\frac{32\sqrt{2}}{\mathrm{\pi }}$

• $\frac{4}{\mathrm{\pi }}$

For a simple pendulum, the graph between T² L and is

• a straight line passing through the origin

• parabola

• circle 

• ellipse

The mstantaneous displacement of a simple harmonic oscillator is given by $\mathrm{y} = \mathrm{A}\hspace{0.17em}\cos \left(\mathrm{\omega t} + \frac{\mathrm{\pi }}{4}\right)$. Its speed will be maximum at the time 

• $\frac{2\mathrm{\pi }}{\mathrm{\omega }}$

• $\frac{\mathrm{\omega }}{2\mathrm{\pi }}$

• $\frac{\mathrm{\omega }}{\mathrm{\pi }}$

• $\frac{\mathrm{\pi }}{4\mathrm{\omega }}$

69.

A particle of mass 5 g is executing simple harmonic motion with amplitude of 0.3 m and time period $\left(\mathrm{\pi }/5\right)$s. The maximumvalue of the force acting on the particle is

• 5 N

• 4 N

• 0.15 N

• 0.3 N

A simple pendulum has a time period T when on the earth's surface and T₂ when taken to a height 2R above the earth's surface where R is the radius ofthe earth. The value of (T₁ /T₂) is

• $\frac{1}{9}$

• $\frac{1}{3}$

• 3

• 9