When the displacement is one-half the amplitude in SHM, the fraction of the total energy that is potential is

• $\frac{1}{2}$

• $\frac{3}{4}$

• $\frac{1}{4}$

• $\frac{1}{8}$

The equation of a simple harmonic motion is X = 0.34 cos (3000 t + 0.74), where X and t are in mm and sec respectively. The frequency of the motion in Hz is

• 3000

• $\frac{3000}{2\mathrm{\pi }}$

• $\frac{0.74}{2\mathrm{\pi }}$

• $\frac{3000}{\mathrm{\pi }}$

The displacement time graph of a particle executing SHM is as shown in the figure.

The corresponding force time graph of the particle is

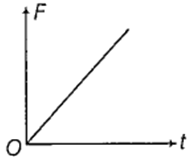
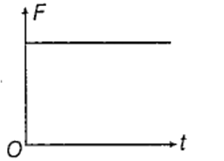
 A simple pendulum has a length l and the mass of the bob is m. The bob is given a charge q coulomb. The pendulum is suspended between the vertical plates of a charged parallel plate capacitor. If E is the electric field strength between the plates, the time period of the pendulum is given by

• $2\mathrm{\pi }\sqrt{\frac{\mathrm{l}}{\mathrm{g}}}$

• $2\mathrm{\pi }\sqrt{\frac{\mathrm{l}}{\sqrt{\mathrm{g} + {\displaystyle \frac{\mathrm{qE}}{\mathrm{m}}}}}}$

• $2\mathrm{\pi }\sqrt{\frac{\mathrm{l}}{\sqrt{\mathrm{g} - {\displaystyle \frac{\mathrm{qE}}{\mathrm{m}}}}}}$

• $2\mathrm{\pi }\sqrt{\frac{\mathrm{l}}{\sqrt{{\mathrm{g}}^2 + {\left({\displaystyle \frac{\mathrm{qE}}{\mathrm{m}}}\right)}^2}}}$

The equation of a simple harmonic wave is given by $\mathrm{y} = 5 \sin \frac{\mathrm{\pi }}{2} \left(100\mathrm{t} - \mathrm{x}\right)$, where x and y are in metre and time is in second. The period of the wave in second will be

• 0.04

• 0.01

• 1

• 5

A simple pendulum is suspended from the ceiling of a lift. When the lift is at rest its time period is T. With what acceleration should the lift be accelerated upwards in order to reduce its period to T/ 2? (g is acceleration due to gravity).

• 2 g

• 3 g

• 4 g

• g

87.

The equation of a simple harmonic wave is given by y = 6 sin 2π (2t − 0.1x), where x and y are in mm and t is in seconds. The phase difference between two particles 2 mm apart at any instant is

• 18°

• 36°

• 54°

• 72°

Two simple harmonic motions are represented by

$$\begin{gathered} {\mathrm{y}}_1 = 5 \left[\sin 2\mathrm{\pi t} + \sqrt{3} \cos 2\mathrm{\pi t}\right] \\ \mathrm{and} {\mathrm{y}}_2 = 5 \sin \left(2\mathrm{\pi t} + \frac{\mathrm{\pi }}{4}\right) \end{gathered}$$

The ratio of their amplitudes is

• 1 : 1 

• 2 : 1

• 1 : 3

• $\sqrt{3} : 1$

A particle executing a simple harmonic motion has a period of 6 s. The time taken by the particle to move from the mean position to half the amplitude, starting from the mean position is

• $\frac{3}{2} \mathrm{s}$

• $\frac{1}{2} \mathrm{s}$

• $\frac{3}{4} \mathrm{s}$

• $\frac{1}{4} \mathrm{s}$

A particle executes SHM with amplitude 0.2 m and time period 24 s. The time required it to move from the mean position to a point 0.1 m from the mean position is

• 12 s

• 2 s

• 8 s

• 3 s