If we study the vibration of a pipe open at both ends, then the following statements is not true

• open end will be anti-node

• Odd harmonics of the fundamental frequency will be generated

• All harmonics of the fundamental frequency will be generated

• All harmonics of the fundamental frequency will be generated

A source of unknown frequency gives 4 beats/s when sounded with a source of known frequency 250 Hz. The second harmonic of the source of unknown frequency gives five beats per second when sounded with a source of frequency 5.13 Hz. The unknown frequency is

• 250 Hz

• 246 Hz

• 240 Hz

• 240 Hz

Out of the following functions representing motion of a particle which represents SHM

• Only (IV) does not represent SHM

• (I) and (III)

• (I) and (II)

• (I) and (II)

A string is stretched between fixed points separated by 75.0 cm. It is observed to have resonant frequencies of 420 Hz and 315 Hz. There are no other resonant frequencies between these two. The lowest resonant frequency for this strings is

• 155 Hz

• 205 Hz

• 10.5 Hz

• 10.5 Hz

A particle is executing a simple harmonic motion. Its maximum acceleration is α and maximum velocity is β. Then, its time period of vibration will be 

• β²/α²

• α/β

• β²/α

• β²/α

Two particle are oscillating along two close parallel straight lines sides by sides, with the same frequency and amplitudes. They pass each other, moving in opposite directions when their displacement is half of the amplitude. The mean position of the two particles lie on a straight line perpendicular to the paths of the two particles.
The phase difference is

• zero

• 2π/3

• π

• π

118.

The displacement of a particle along the x-axis is given by x = a sin² ωt. The motion of the particle corresponds to 

• simple of harmonic motion of frequency ω/π

• simple harmonic motion of frequency 3ω/2π

• non simple harmonic motion

• non simple harmonic motion

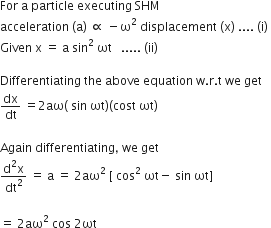
The period of oscillation of mass M suspended from a spring of negligible mass is T. If along with it another mass M is also suspended, the period of oscillation will now be

• T

• 

• 2T

• 2T

A simple pendulum performs simple harmonic motion about x = 0 with an amplitude a and time period T. the speed of the pendulum at x = a/2 will be

• 

• πa / T

• 3π²a / T

• 3π²a / T