 Multiple Choice Questions
Multiple Choice QuestionsA rectangular block of mass m and area of cross-section A floats in a liquid of density ρ. If it is given a small vertical displacement from equilibrium it undergoes oscillation with a time period T. Then:




A transistor-oscillator using a resonant circuit with an inductor L (of negligible resistance) and a capacitor C in series produce oscillations of frequency f. If L is doubled and C is changed to 4C, the frequency will be
f/4
8f


The potential energy of a long spring when stretched by 2 cm is U. If the spring is stretched by 8cm the potential energy stored in it is
4U
8U
16U
16U
C.
16U
Let extension produced in a spring be x initially in stretched condition spring will have potential energy
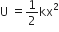
where k is spring constant or force constant.
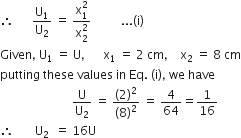
A particle executes linear simple harmonic motion with an amplitude of 3 cm. When the particle is at 2 cm from the mean position, the magnitude of its velocity is equal to that of its acceleration. Then its time period in seconds is




A spring of force constant k is cut into lengths of ratio 1: 2 : 3. They are connected in series and the new force constant is k'. Then they are connected in parallel and force constant is k''. Then k' : k'' is
1:6
1:9
1:11
1:11
Two blocks A and B of masses 3m and m respectively are connected by a massless and inextensible string. The whole system is suspended by a massless spring as shown in the figure. The magnitudes of acceleration of A and B immediately after the string is cut, are respectively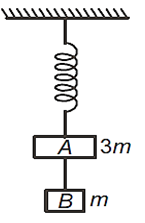
g,g/3
g/3, g
g,g
g,g
A tuning fork is used to produce resonance in a glass tube. The length of the air column in this tube can be adjusted by a variable piston. At room temperature of 27ºC two successive resonances are produced at 20 cm and 73 cm of column length. If the frequency of the tuning fork is 320 Hz, the velocity of sound in air at 27ºC is
330 m/s
339 m/s
300 m/s
350 m/s
A pendulum is hung from the roof of a sufficiently high building and is moving freely to and fro like a simple harmonic oscillator. The acceleration of the bob of the pendulum is 20 m/s2 at a distance of 5 m from the mean position. The time period of oscillation is
2πs
π s
1s
2s
A particular of mass m is executing oscillation about the origin on X- axis. Its potential energy is V(x) = K |x|3. Where K is a positive constant. If the amplitude of oscillation is a, then its time period T is proportional to
a
a3/2
The displacement of a particle along the x-axis is given by x = a sin2 ωt. The motion of the particle corresponds to
Simple harmonic motion of frequency ω/π
Simple harmonic motion of frequency 3ω/2π
non-simple harmonic motion
Simple harmonic motion of frequency ω/2π
