 Multiple Choice Questions
Multiple Choice QuestionsMoment of inertia of a thin uniform rod rotating about the perpendicular axis passing through its centre is I. Ifthe same rod is bent into a ring and its moment of inertia about its diameter is I', then the ratio is
Which of the points is likely position of the centre of mass of the system shown in the figure ?

A
D
B
C
Two balls are thrown simultaneously in air. The acceleration of the centre of mass of the two balls when in air
is equal to g (acceleration due to gravity)
depends on the speeds of the two balls
depends on the masses of the two balls
depends on the direction of motion of the two balls
From a disc of radius R and mass M, a circular hole of diameter R, whose rim passes through the centre is cut. What is the moment of inertia of the remaining part of the disc, about a perpendicular axis, passing through the centre?
13 MR2/32
11MR2/32
9MR2/32
15MR2/32
A disc and a sphere of the same radius but differnt masses roll off two inclined planes of the same altitude and length. which one of the two objects gets to the bottom of the plane first?
Sphere
Both reach at the same time
Depends on their masses
Disc
A uniform circular disc of radius 50 cm at rest is free to turn about an axis which is perpendicular to its plane and passes through its centre. It is subjected to a torque which produces a constant angular acceleration of 2.0 rad/sec2. It's net acceleration in m/s2 at the end of 2.0 s is a approximately.
7.0
6.0
3.0
8.0
A rod of weight w is supported by two parallel knife edges A and B and is in equilibrium in a horizontal position. The knives are at distance d from each other. The centre of mass of the rod is at distance x from A. The normal reaction on A is


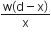
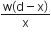
A mass m moves in a circle on a smooth horizontal plane with velocity vo at a radius Ro. The mass is attached to a string which passes through a smooth hole in the plane as shown.
The tension in the string is increased gradually and finally m moves in a circle in a circle of radius Ro/2. The final values of the kinetic energy is
mv02
1/4mvo2
2mvo2
2mvo2
Three identical spherical shells, each of mass m and radius r are placed as shown in the figure. Consider an axis XX', which is touching to two shells and passing through the diameter of the third shell. Moment of inertia of the system consisting of these three spherical shells about XX' axis is
11/5 mr2
3 mr2
16/5 mr2
16/5 mr2
D.
16/5 mr2
The total moment of inertia of the system is 
I = I1 +I2 +I3
