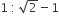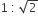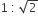Previous Year Papers

Download Solved Question Papers Free for Offline Practice and view Solutions Online.

Test Series

Take Zigya Full and Sectional Test Series. Time it out for real assessment and get your results instantly.

Test Yourself

Practice and master your preparation for a specific topic or chapter. Check you scores at the end of the test.

Geometry - Triangles

Multiple Choice Questions

41.

A point D is taken from the side BC of a right-angled triangle ABC, where AB is hypotenuse. Then

AB² + CD² = BC² + AD²
CD² + BD² = 2 AD²
AB² + AC² = 2AD²
AB² + AC² = 2AD²

540 Views

42.

An isosceles triangle ABC is right-angled at B. D is a point inside the triangle ABC. P and Q are the feet of the perpendiculars drawn from D on the sides AB and AC respectively of ΔABC. If AP = a cm, AQ = b cm and ∠BAD = 15°, sin 75° =

$fraction numerator 2 straight b over denominator square root of 3 space straight a end fraction$
$fraction numerator straight a over denominator 2 straight b end fraction$
$fraction numerator square root of 3 straight a over denominator 2 straight b end fraction$
$fraction numerator square root of 3 straight a over denominator 2 straight b end fraction$

974 Views

43.

D and E are two points on the sides AC and BC respectively of Δ ABC such that DE = 18 cm, CE = 5 cm and ∠DEC = 90°, If tan ∠ABC = 3.6, then AC : CD =

BC : 2 CE
2 CE : BC
2 BC : CE
2 BC : CE

1793 Views

44.

D is a point on the side BC of a triangle ABC such that $AD space perpendicular space BC$ . E is a point on AD for which AE : ED = 5 : 1. If $angle BAD space equals space 30 degree$ and then $tan left parenthesis angle ACB right parenthesis space equals space 6 space tan space space left parenthesis angle DBE right parenthesis comma$ then $angle ACB space equals$

30°
45°
60°
40°

308 Views

45.

In ΔABC, P and Q are the middle points of the sides AB and AC respectively. R is a point on the segment PQ such that PR : RQ = 1 : 2. If PR = 2cm, the BC =

4 cm
2 cm
12 cm
12 cm

229 Views

46.

The angles of a triangle are in Arithmetic Progression. The ratio of the least angle in degrees to the number of radians in the greatest angle is $60 thin space colon space straight pi$ . The angles in degrees are

30°, 60°, 90°
35°, 55°, 90°
40°, 50°, 90°
40°, 50°, 90°

225 Views

47.
If the incentre of an equilateral triangle lies inside the triangle and its radius is 3 cm, then the side of the equilateral triangle is

$9 square root of 3 space cm$
$6 square root of 3 space cm$
$3 square root of 3 space cm$
$3 square root of 3 space cm$

6 square root of 3 space cm

In radius = $fraction numerator Side over denominator 2 square root of 3 end fraction$
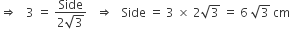
$rightwards double arrow space space space 3 space equals space fraction numerator Side over denominator 2 square root of 3 end fraction space space space rightwards double arrow space space space Side space equals space 3 space cross times space 2 square root of 3 space equals space 6 space square root of 3 space cm$

171 Views

48.

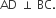Suppose ΔABC be a right-angled triangle where $angle straight A space equals space 90 degree$ and $AD space perpendicular space BC.$ If Δ ABC = 40 cm², ΔACD = 10 cm² and 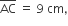$AC with bar on top space equals space 9 space cm comma$ then the length of BC is

12 cm
18 cm
4 cm
4 cm

164 Views

49.

In ΔABC, D and E are points on AB and AC respectively such that DE || BC and DE divides the ΔABC into two parts of equal areas. Then ratio of AD and BD is

1 : 1
$1 space colon space square root of 2 minus 1$
$1 space colon space square root of 2$
$1 space colon space square root of 2$

433 Views

50.

I is the incentre of a triangle ABC. If $angle ABC space equals space 65 degree$ and $angle ACB space equals space 55 degree comma$ then the value of $angle BIC$ is