 Multiple Choice Questions
Multiple Choice QuestionsG is the centroid of the equilateral Δ ABC, if AB = 9 cm, then AG is equal to:

3 cm

6 cm
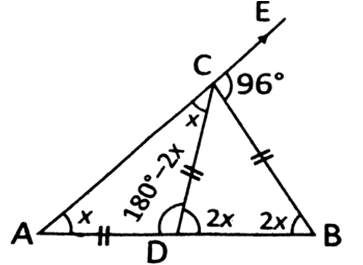
In the figure (not drawn to scale) given below, if AD = DC = BC and  , then
, then  then
then  is
is
32°
84°
64°
96°
C.
64°
As we know that in triangle rule property, sum of exterior angle is equal to sum of opposite interior angles
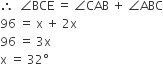
Thus,
In ΔABC, the medians AD and BE meet at G. The ratio of the areas of ΔBDG and the quadrilateral GDCE is:
1 : 2
1 : 3
2 : 3
3 : 4
BE and CF are two altitudes of a Δ ABC. If AB = 6 cm, AC = 5 cm and CF = 4 cm, then the length of BE is
4.8 cm
7.5 cm
3.33 cm
5.5 cm
O is the ortho-centre of Δ ABC, and if ∠BOC = 110°, then ∠BAC will be
110°
70°
100°
90°
In a right angled triangle if hypotense is 20 cm and ratio of other two sides is 4 : 3, the length of the sides are
4 cm and 3 cm
8 cm and 6 cm
12 cm and 9 cm
16 cm and 12 cm
D and E are the points on the sides AB and AC respectively of a Delta; ABC and AD = 8 cm, DB = 12 cm, AE = 6 cm and EC = 9 cm, then BC is equal to
DE = 2/5 DE
DE = 5/2 DE
DE = 3/2 DE
DE = 3/5 DE
Which one of the following combination of measurements can form the sides of a triangle?
9 cm, 6cm, 2cm
11 cm, 3 cm, 12 cm
3 cm, 5cm, 8cm
5cm, 7cm, 13cm
