 Multiple Choice Questions
Multiple Choice QuestionsIn Δ ABC, ∠BAC = 90° and AD is perpendicular to BC. If AD = 6cm and BD = 4 cm, then the length of BC is
10 cm
12 cm
13 cm
15 cm
The point equidistant from the sides of a triangle is called:
Circumcenter
Incentre
Orthocentre
Centroid
In Δ ABC and Δ DEF, if ∠A = 50°, ∠B = 70°, ∠C = 60°, ∠D = 60°, ∠E = 70° and ∠F = 50° then
Δ ABC ~ Δ FED
Δ ABC ~ Δ DFE
Δ ABC ~ Δ EDF
Δ ABC ~ Δ DEF
The point where three medians of a triangle meet is called
Centroid
Incentre
Circumcentre
Orthocentre
Δ ABC a right-angled triangle and D, E are midpoints of AB and BC respectively. Then the ratio of the area of Δ ABC and the area of trapezium ADEC is:
5 : 3
4 : 1
8 : 5
4 : 3
D.
4 : 3
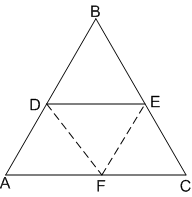
By mid-point theorem:
area (Δ ABC) = ar (Δ ADF) = 1 : 1/4
Also,
ar (Δ ADF) = ar(Δ DFE) = ar(Δ EFC) = 1/4
ar(trapezium) = 1/4 + 1/4 + 1/4 = 3/4
∴ ar (Δ ABC) : ar (trapezium ADEC) = 1 : 3/4 = 4 : 3
In an isosceles triangle ABC, AB = AC, XY || BC. If ∠A = 30°, then ∠BXY = ?
75°
30°
150°
105°
If 'O' is the incentre of the Δ PQR. If ∠POR = 115° then value of ∠PQR is
40°
65°
50°
25°
The in-radius of triangle is 4 cm and its area is 34 sq cm. The perimeter of the triangle is
8.5 cm
17 cm
34 cm
20 cm
The area of a Δ ABC is 10.8 cm2. If CP = PB and 2AQ = QB, then the area of the Δ APQ is:
3.6 cm2
0.9 cm2
2.7 cm2
1.8 cm2
