101.

In Δ ABC,   if   and AB = AC,  then  is

• 30°

• 60°

• 45°

• 25°

In a ΔPQR,  S and T are the points on PQ and PR respectively, such that ST || QR and 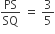, PR = 6cm, then PT is

• 2 cm

• 2.25 cm

• 3.5 cm

• 4 cm

If the ratio of area of two similar triangles is 9 : 16, then the ratio of their corresponding sides is

• 3 : 5

• 3 : 4

• 4 : 5

• 4 : 3

If l is the in-centre of Δ ABC and ∠A = 60°, then the value of ∠BIC is

• 100°

• 120°

• 150°

• 110°

The external bisectors of ∠B and ∠C of Δ ABC meet at point P. If Δ BAC = 80°, then ∠BPC is

• 50°

• 40°

• 80°

• 100°

Let BE and CF be the two medians of a Δ ABC and G be their intersection. Also let EF cut AG at O. Then, AO : OG is

• 1 : 1

• 1 : 2

• 2 : 1

• 3 : 1

In an obtuse-angled triangle ABC, ∠A is the obtuse angle and O is the orthocentre. If ∠BOC = 54°, then ∠BAC is

• 108°

• 126°

• 136°

• 116°

If G is the centroid and AD, BE, CF are three medians of Δ ABC with area 72 cm², then the area of Δ BDG is

• 16 cm²

• 24 cm²

• 8 cm²

• 12 cm²

The three medians AD, BE and CF of a Δ ABC intersect at point G. If the area of Δ ABC is 60 cm², then the area of the quadrilateral BDGF is

• 15 cm²

• 20 cm²

• 30 cm²

• 10 cm²

Consider Δ ABD such that ∠ADB = 20° and C is a point on BD such that AB = AC and CD = CA. Then, the measure of ∠ABC is

• 45°

• 60°

• 30°

• 40°