G is the centroid of the equilateral ΔABC. If AB = 10 cm, then length of AG is

In triangle ABC a straight line parallel to BC intersects AB and AC at D and E respectively. If AB = 2AD then DE : BC is

• 2 : 3

• 2 : 1

• 1 : 2

• 1 : 2

ABC is an isosceles triangle such that AB = AC and AD is the median to the base BC with ∠ABC = 35°.

Then ∠BAD is

• 35°

• 55°

• 70°

• 70°

A man goes 24 m due west and then 10 m due north. Then the distance of him from the starting point is

• 17 m

• 26 m

• 28 m

• 28 m

a and b are two sides of adjacent to the right angle of a right-angled and p is the perpendicular drawn to the hypotenuse from the opposite vertex. Then p² is equal to

If the sum and difference of two angles are 135° and  respectively, then the value of the angles in degree measure are

• 70°, 65°

• 75°, 60°

• 45°, 90°

• 45°, 90°

37.  are three angles of a triangle, If 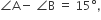 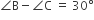, then are

• 80°,  60°, 40°

• 70°, 50°, 60°

• 80°, 65°, 35°

• 80°, 65°, 35°

If ABC is an equilateral triangle and D is a point on BC such that 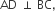 then

• AB : BD = 2 : 1

• AB : BD = 1 : 2

• AB : BD = 2 : 1

• AB : BD = 2 : 1

Δ ABC is an isosceles triangle and  Draw  and find the length of 

In a right-angled triangle, the product of two sides is equal to half of the square of the third side i.e. hypotenuse. One of the acute angles must be

• 60° 

• 30° 

• 45° 

• 45°