 Long Answer Type
Long Answer TypeA small firm manufactures gold rings and chains. The total number of rings and chains manufactured per day is at most 24. It takes 1 hour to make a ring and 30 minutes to make a chain. The maximum number of hours available per day is 16. If the profit on a ring is Rs. 300 and that on a chain is Rs. 190, find the number of rings and chains that should be manufactured per day, so as to earn the maximum profit. Make it as an L.P.P. and solve it graphically
Let x be number of gold rings and y be number of chains manufactured
L.P.P. is
Max Z = 3000 x + 190 y
Substitute in x + y 24
Feasible region
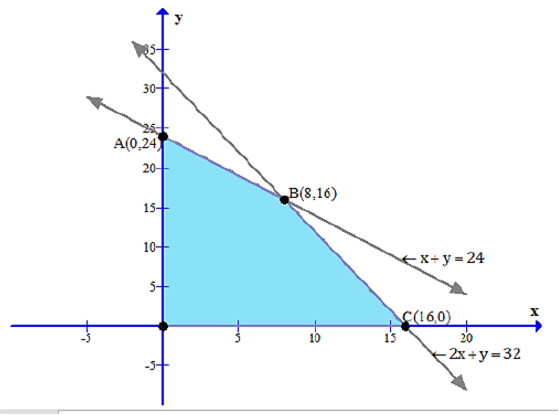
| Corner points |
Value of Z = 300x 190y |
|
| A ( 0, 24 ) | 4560 | |
| B ( 8, 16 ) | 5440 | Maximum |
| C ( 16, 0 ) | 4800 | |
| O ( 0, 0 ) | 0 |
Hence to make the maximum profit, 8 gold rings and 16 chains must be manufactured.
A card form a pack of 52 cards is lost. From the remaining cards of the pack, two cards are drawn at random and are found to be both clubs. Find the probability of the lost card being of clubs.
From a lot of 10 bulbs, which includes 3 defectives, a sample of 2 bulbs is drawn at random. Find the probability distribution of the number of defective bulbs.
Write the vector equations of the following lines and hence determine the distance between them:
