Short Answer Type
Long Answer TypeThe current flowing through a conductor is given by I = neAvd.Â
(i) Identify each term in the equation.
(ii) Obtain an expression for vd, if the current flowing through the conductor of length I has its ends maintained at a potential difference of V volts.
(i) Write an expression for Biot-Savart’s law in the vector form. Write an expression for the magnetic field at the centre of a circular coil of radius R, with N turns and carrying a current I.Â
(ii) A helium nucleus completes one round of a circle of radius 0.8 m in 2 seconds. Find the magnetic field at the centre of the circle.
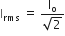 where Irms is the root mean square value of alternating current and I0 is its peak value.
(i) Derive an expression for the fringe width ‘y’ in Young’s double slit experiment. Use X as the wavelength of the monochromatic source, D as the distance of the screen from the slits and d as the distance of separation between the slits.
(ii) How does the fringe pattern change if the monochromatic source of light in the above experiment is replaced by a white source of light ?
(i)
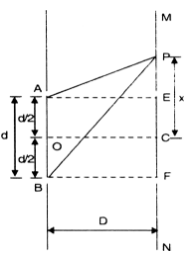
Expression for fringe width : Considering a point P at a distance x from C. The path difference between two waves arriving at P.
  = BP -APÂ
  
Â
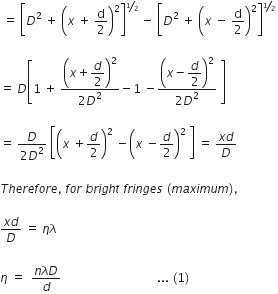
where n = 0, 1, ....
for, and dark fringe (minima)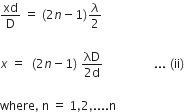
So fringe width Y is defined as the distance between two consecutive dark fringe or distance between two consecutive bright fringe.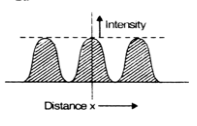
So,Â
  Y = xn - xn - 1
 
Â
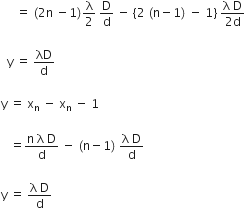
ii)
When we use a source of white light containing light of different colours i.e. (different wavelength X), they at a particular point, constructive interference may be satisfied only for some particular value of X.
Thus, the colour corresponding to this value of X alone shall be visible at that point. Hence the interference fringe will be coloured.
Switch
