 Multiple Choice Questions
Multiple Choice QuestionsThe set of all real values of for which the quadratic equation (2 + 1) x2 – 4x + 2 = 0 always have exactly one root in the interval (0, 1) is :
( - 3, - 1)
(0, 2)
(1, 3)
(2, 4)
Let p, q, r be three statements such that the truth value of is F. Then the truth values of p, q, r are respectively :
T, T, F
T, T, T
T, F, T
F, T, F
The Plane which bisects the line joining the points (4, – 2, 3) and (2, 4, – 1) at right angles also passes through the point :
(0, - 1, 1)
(4, 0, - 1)
(4, 0, 1)
(0, 1, - 1)
B.
(4, 0, - 1)
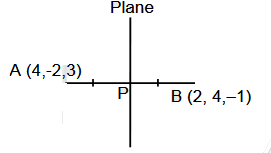
Mid point P = (3, 1, 1)
Normal of plane is along the line AB.
D.R.’s of normal = 4 – 2, – 2 – 4, 3 – ( – 1) = 2, – 6, 4 = 1, – 3, 2
Plane 1(x – 3) – 3(y – 1) + 2(z – 1) = 0
x – 3y + 2z – 2 = 0
If z1, z2 are complex numbers such that Re(z1) = |z1 = 1| and Re(z2) = |z2 = 1| and arg (z1 – z2) = , then Im (z1 + z2) is equal to :
Let e1 and e2 be the eccentricities of the ellipse, respectively satisfying e1e2 = 1. If are the distances between the foci of the ellipse and the foci of the hyperbola respectively, then the ordered pair is equal to:
(8, 10)
(8, 12)
