Dimensional formula for the universal gravitational constant G is

• [M^-1L²T^-2]

• [M⁰L⁰T⁰]

• [M^-1L³T^-2]

• [M^-1L³T^-1]

A body is projected vertically upwards. The times corresponding to height h while ascending and while descending are t₁ and t₂ respectively. Then the velocity of projection is (g is acceleration due to gravity)

• $\mathrm{g}\sqrt{{\mathrm{t}}_1{\mathrm{t}}_2}$

• $\frac{{\mathrm{gt}}_1{\mathrm{t}}_2}{{\mathrm{t}}_1 + {\mathrm{t}}_2}$

• $\frac{\mathrm{g}\sqrt{{\mathrm{t}}_1{\mathrm{t}}_2}}{2}$

• $\frac{\mathrm{g}\left({\mathrm{t}}_1 + {\mathrm{t}}_2\right)}{2}$

A mass of 10 kg is suspended from a spring balance. It is pulled aside by a horizontal string so that it makes an angle of 60° with the vertical. The new reading of the balance is

• 20 kg-wt

• 10 kg-wt

• $10\sqrt{3} \mathrm{kg}-\mathrm{wt}$

• $20\sqrt{3} \mathrm{kg}-\mathrm{wt}$

A body of mass 4 kg is accelerated upon by a constant force, travels a distance of 5 m in the first second and a distance of 2 m in the third second. The force acting on the body is

• 2 N

• 4 N

• 6 N

• 8 N

If μ₀ is permeability of free space and ε₀ is permittivity of free space, the speed of light in vacuum is given by

• $\sqrt{{\mathrm{\mu }}_0{\mathrm{\epsilon }}_0}$

• $\sqrt{\frac{{\mathrm{\mu }}_0}{{\mathrm{\epsilon }}_0}}$

• $\sqrt{\frac{1}{{\mathrm{\mu }}_0{\mathrm{\epsilon }}_0}}$

• $\sqrt{\frac{{\mathrm{\epsilon }}_0}{{\mathrm{\mu }}_0}}$

A body weighs 50 g in air and 40 g in water. How much would it weigh in a liquid of specific gravity 1.5 ?

• 30 g

• 35 g

• 65 g

• 45 g

A simple pendulum is suspended from the ceiling of a lift. When the lift is at rest its time period is T. With what acceleration should the lift be accelerated upwards in order to reduce its period to T/ 2? (g is acceleration due to gravity).

• 2 g

• 3 g

• 4 g

• g

8.

If γ is the ratio of specific heats and R is the universal gas constant, then the molar specific heat at constant volume C_V is given by

• γR

• $\frac{\left(\mathrm{\gamma } - 1\right) \mathrm{R}}{\mathrm{\gamma }}$

• $\frac{\mathrm{R}}{\mathrm{\gamma } - 1}$

• $\frac{\mathrm{\gamma R}}{\mathrm{\gamma } - 1}$

An ideal gas is taken via path ABCA as shown in figure. The net work done in the whole cycle is

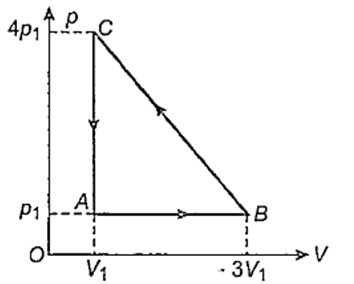
• 3p₁V₁

• − 3p₁V₁

• 6p₁V₁

• Zero

In which of the processes, does the internal energy of the system remain constant ?

• Adiabatic 

• Isochoric

• Isobaric

• Isothermal