 Multiple Choice Questions
Multiple Choice QuestionsThe displacement x of a particle varies with time t as x = ae-αt + beβt where a, b, and β are positive constants. The velocity of the particle will
decrease with time
be independent of
drop to zero when
increase with time
If A + B = C and that C is perpendicular to A. What is the angle between A and B, if
rad
rad
rad
rad
A body is whirled in a horizontal circle of radius 25 cm. It has an angular velocity of 13 rad/s. What is its linear velocity at any point on circular path?
2 m/s
3 m/s
3.25 m/s
4.25 m/s
Two wires are stretched through same distance. The force constant ofsecond wire is half as that of the first wire. The ratio of work done to stretch first wire and second wire will be
2 : 1
1 : 2
3 : 1
1 : 3
A particle slides down on a smooth incline of inclination 30°, fixed in an elevator going up with an acceleration 2 m/s2. The box of incline has a length 4m. The time taken by the particle to reach the bottom will be

( 8/9 ) √3 s
( 9/8 ) √3 s
( 4/3 ) √(√3/2 ) s
( 3/4 ) √(√3/2 ) s
A stone projected with a velocity u at an angle θ with the horizontal reaches maximum height H1. When it is projected with velocity u at an angle with the horizontal, it reaches maximum height H2. The relation between the horizontal range R of the projectile, H1 and H2 is
R =
R = 4 ( H1 - H2 )
R = 4( H1 + H2 )
R =
A light string passes over a frictionless pulley. To one of its ends a mass of 8 kg is attached. To its other end two masses of 7 kg each are attached. The acceleration of the system will be

10.2 g
5.10 g
20.36 g
0.27 g
D.
0.27 g
free body diagram,
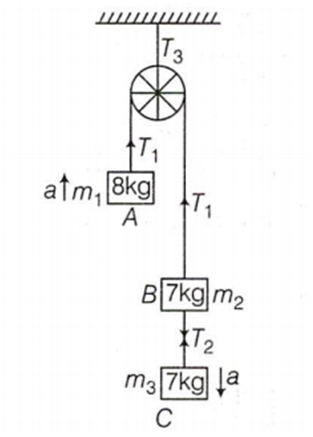
For body A, having mass m1 forces are given by
m1a = T1 - m1 g ....(i)
For body B
m2a = m2 g + T2 - T1 .....(ii)
For body C
m3 a = m3g - T2 ......(iii)
On solving Eqs. (i), (ii) and (iii), we get
a =
As m1 = 8 kg, m2 = m3 = 7 kg
a =
a =
a = 0.27 g
A sphere of mass m moving with velocity v hits inelastically with another stationary sphere of same mass. The ratio of their final velocities will be (in terms of e)
Particles of masses m, 2m, 3m, ... , nm are placed on the same line at distances L, 2L, 3L, ... , nL from O. The distance of centre of mass from O is
![]()
![]()
![]()
![]()
A ball of radius R rolls without slipping. Find the fraction of total energy associated with its rotational energy, if the radius of the gyration of the ball about an axis passing through its centre of mass is K.
