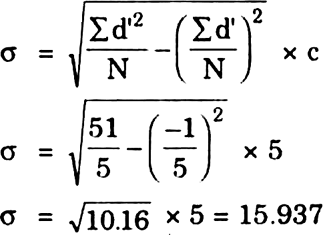Calculate the standard deviation of the following values by following methods:
(i) Actual Mean Method, (ii) Assumed Mean Method, (iii) Direct Method, (iv) Step Deviation Method.
5, 10, 25, 30, 50.
(i) Calculation of Standard Deviation by Actual Mean Method :
|
X |
d |
d2 |
|
5 |
–19 |
361 |
|
10 |
–14 |
196 |
|
25 |
+1 |
1 |
|
30 |
+6 |
36 |
|
50 |
+26 |
676 |
|
ΣX = 120 |
0 |
Σd2 = 1270 |
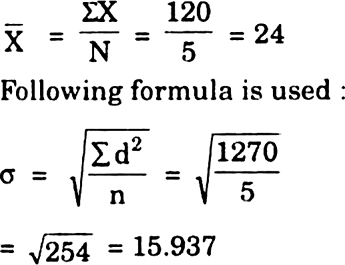
(ii) Calculation of Standard Deviation by Assumed Mean Method :
|
X |
d |
d2 |
|
5 |
–20 |
400 |
|
10 |
–15 |
225 |
|
25 |
0 |
0 |
|
30 |
+5 |
25 |
|
50 |
+25 |
625 |
|
–5 |
1275 |
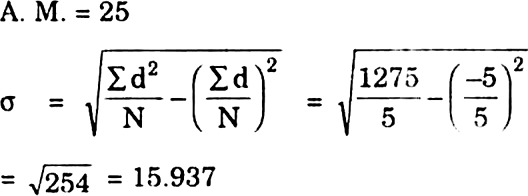
(iii) Calculation of Standard Deviation by Direct Method : Standard Deviation can also be calculated from the values directly, i.e., without taking deviations, as shown below :
|
X |
x2 |
|
5 |
25 |
|
10 |
100 |
|
25 |
625 |
|
30 |
900 |
|
50 |
2500 |
|
ΣX = 120 |
ΣX2 = 4150 |
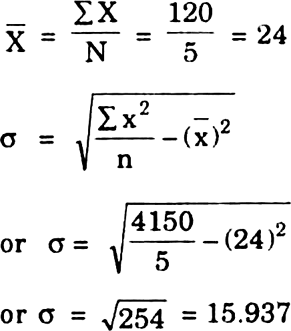
(iv) Calculation of Standard Deviation by Step Deviation Method : The values are divisible by a common factor, they can be so divided and standard deviation can be calculated from the resultant values as follows :
Since all the five values are divisible by a common factor 5, we divide and get the following values :
|
x |
x2 |
d |
d2 |
|
5 |
1 |
–3.8 |
14.44 |
|
10 |
2 |
–2.8 |
7.84 |
|
25 |
5 |
+0.2 |
0.04 |
|
30 |
6 |
+1.2 |
1.44 |
|
50 |
10 |
+5.2 |
27.04 |
|
N = 5 |
0 |
50.80 |
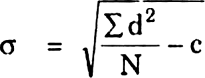
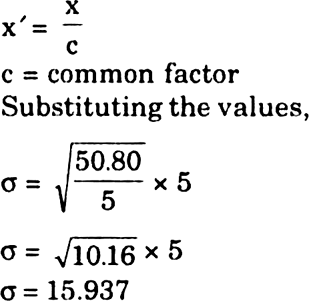
Alternative Method : Alternatively, instead of dividing the values by a common factor, the deviations can be divided by a common factor. Standard Deviation can be calculated as shown below :
|
x |
d |
d' |
d2 |
|
5 |
–20 |
–4 |
16 |
|
10 |
–15 |
–3 |
9 |
|
25 |
0 |
0 |
0 |
|
30 |
+5 |
+1 |
1 |
|
50 |
+25 |
+5 |
25 |
|
N = 5 |
–1 |
51 |
Deviations have been calculated from an arbitrary value 25. Common factor of 5 has been used to divide deviations.