Pre Boards

Practice to excel and get familiar with the paper pattern and the type of questions. Check you answers with answer keys provided.

Sample Papers

Download the PDF Sample Papers Free for off line practice and view the Solutions online.

CBSE Class 10 Mathematics Solved Question Paper 2017

Short Answer Type

11.

Find the sum of n terms of the series $open parentheses 4 minus 1 over straight n close parentheses space plus open parentheses 4 minus 2 over straight n close parentheses space plus open parentheses 4 minus 3 over straight n close parentheses space plus.........$

11126 Views

12.

If the equation (1 + m²) x² + 2mcx + c² – a² = 0 has equal roots then show that c² = a² (1 + m²).

3662 Views

13.

The 3/4th part of a conical vessel of internal radius 5 cm and height 24 cm is full of water. The water is emptied into a cylindrical vessel with internal radius 10 cm. Find the height of water in a cylindrical vessel.

4703 Views

14.

In the given figure, OACB is a quadrant of a circle with centre O and radius 3.5 cm. If OD = 2 cm, find the area of the shaded region.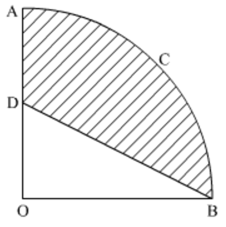

4315 Views

15.

Two tangents TP and TQ are drawn to a circle with centre O from an external point T. Prove that ∠PTQ = 2 ∠OPQ.

3153 Views

16.

Show that ΔABC, where A(–2, 0), B(2, 0), C(0, 2) and ΔPQR where P(–4, 0), Q(4, 0), R(0, 2) are similar triangles.

2835 Views

17.

The area of a triangle is 5 sq units. Two of its vertices are (2, 1) and (3, –2). If the third vertex is (7/2, y), find the value of y.

5380 Views

18.
Two different dice are thrown together. Find the probability that the numbers obtained
(i) have a sum less than 7
(ii) have a product less than 16
(iii) is a doublet of odd numbers.

The outcomes when two dice are thrown together are
(1,1), (1,2), (1,3), (1,4), (1,5), (1,6)
(2,1), (2,2), (2,3), (2,4), (2,5), (2,6)
(3,1), (3,2), (3,3), (3,4), (3,5), (3,6)
(4,1), (4,2), (4,3), (4,4), (4,5), (4,6)
(5,1), (5,2), (5,3), (5,4), (5,5), (5,6)
(6,1), (6,2), (6,3), (6,4), (6,5), (6,6)
Total number of outcomes = 36

(i) Let A be the event of getting the numbers whose sum is less than 7.

The outcomes in favour of event A are (1, 1), (1,2), (1,3), (1,4), (1,5), (2,1), (2,2), (2,3), (2,4), (3,1), (3,2), (3,3), (4,1), (4,2) and (5,1).
Number of favourable outcomes = 15
$therefore space straight P left parenthesis straight A right parenthesis space equals space fraction numerator Number space of space favourable space outcomes over denominator Total space number space of space outcomes end fraction space equals space 15 over 36 space equals space 5 over 12$

(ii) Let B be the event of getting the numbers whose product is less than 16.

The outcomes in favour of event B are (1,1), (1,2), (1,3), (1,4), (1,5), (1,6), (2,1), (2,2), (2,3), (2,4), (2,5), (2,6), (3,1), (3,2), (3,3), (3,4), (3,5), (4,1), (4,2), (4,3), (5,1), (5,2), (5,3), (6,1) and (6,2).

Number of favourable outcomes = 25

$therefore space straight P left parenthesis straight A right parenthesis space equals space fraction numerator Number space of space favourable space outcomes over denominator Total space number space of space outcomes end fraction space equals space 25 over 36 space$

iii) Let C be the event of getting the numbers which are doublets of odd numbers.

The outcomes in favour of event C are (1,1), (3,3) and (5,5).

Number of favourable outcomes = 3
$therefore space straight P left parenthesis straight A right parenthesis space equals space fraction numerator Number space of space favourable space outcomes over denominator Total space number space of space outcomes end fraction space equals space 3 over 36 space equals space 1 over 12 space$

9211 Views

19.

A moving boat is observed from the top of a 150 m high cliff moving away from the cliff. The angle of depression of the boat changes from 60° to 45° in 2 minutes. Find the speed of the boat in m/h.

7636 Views