 Multiple Choice Questions
Multiple Choice QuestionsA granite block of 2m × 5m × 3m size into 5cm thick slabs of 2 m × 5m size. These slabs are laid over a 2m wide pavement. What is the length of the pavement that can be covered with these slabs?
100 m
200 m
300 m
500 m
What is the next number in this “see and tell” sequence?
1 11 21 1211 1112211 …….
312211
1112221
1112222
1112131
A vertical pole of length a stands at the centre of a horizontal regular hexagonal ground of side a. A rope that is fixed taut in between a vertex on the ground and the tip of the pole has a length
a
A peacock perched on the top of a 12 m high tree spots a snake moving towards its hole at the base of the tree from a distance equal to thrice the height of the tree. The peacock flies towards the snake in straight line and they both move at the same speed. At what distance from the base of the tree will the peacock catch the snake?
16 m
18 m
14 m
12m
The cities of a country are connected by intercity roads. If a city is directly connected to an odd number of other cities, it is called an odd city. If a city is directly connected to an even number of other cities, it is called an even city. Then which of the following is impossible?
There are an even number of odd cities.
There are an odd number of odd cities.
There are an even number of even cities.
There are an odd number of even cities.
B.
There are an odd number of odd cities.
As each road connects two cities, connectedness value (number of cities it is connected to) of each of the two cities increase by one. In other words, each road or each edge in a connected graph adds to the total value of connectedness by 2. If there are n edges, total connectedness value would be 2n.
If a network of nodes, the number of nodes with odd number of incident edges is odd, the total of connectedness values of those nodes would be odd which is impossible.
In the figure angle ABC = /2
AD = DE = EB
What is the ratio of the area of ADC to that of CDB?
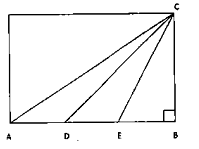
1 : 1
1 : 2
1 : 3
1 : 4
A string of diameter 1mm is kept on a table in the shape of a close flat spiral, i.e. a spiral with no gap between the turns. The area of the table occupied by the spiral is 1 m2. Then the length of the string is
10 m
102 m
103 m
106 m
In the figure below, angle ABC = /2. I, II, III are the areas of semicircles on the sides opposite angles B, A and C respectively. Which of the following is always true?
II2 + III2 = I2
II + III = I
II2 + III2 > I2
II + III < I
