 Short Answer Type
Short Answer TypeTarun bought and article for Rs. 8000 and spent Rs. 1000 for transportation. He marked the article Rs. 11,700 and sold it to a customer. If the customer had to pay 10% sales tax, find:
(i) the customer’s price
(ii) Tarun’s profit percent.
Mr. Gupta opened a recurring deposit account in a bank. He deposited Rs. 2500 per month for two years. At the time of maturity he got Rs. 67,500. Find:
(i) the total interest earned by Mr. Gupta.
(ii)the rate of interest per annum.
Nikita invests Rs. 6000 for two years at a certain rate of interest compounded annually. At the end of first year it amounts to Rs. 6720. Calculate:
(i) the rate of interest.
(ii) the amount at the end of the second year.
A and B are two points on the x – axis and y-axis respectively. P (2, −3) is the mid- point of AB. Find the:
(i) coordinates of A and B
(ii) slope of line AB.
(iii) equation of line AB.

Cards marked with numbers 1, 2, 3, 4… 20 are well shuffled and a card is drawn at random. What is the probability that the number on the card is:
(i) A prime number,
(ii) A number divisible by 3,
(iii)A perfect square?
(Use graph paper for this question)
A(0, 3), B(3, −2) and O(0, 0) are the vertices of triangle ABO.
(i) Plot the triangle on a graph sheet taking 2 cm = 1 unit on both the axes.
(ii) Plot D the reflection of B in the Y axis, and write its co-ordinates.
(iii) Give the geometrical name of the figure ABOD.
(iv) Write the equation of the line of symmetry of the figure ABOD.
(i) AOB is shown in the graph.
(ii) The reflection of B in Y- axis is given by D (−3, −2)
(iii) Figure ABOD is a tetrahedron.
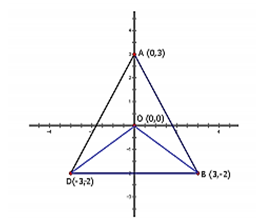
(iv) Equation of line of symmetry of figure ABOD is x = 0, i.e. y-axis.
When divided by x – 3 the polynomials x3 – px2 + x + 6 and 2x3 – x2 – (p + 3)x – 6 leave the same remainder. Find the value of ‘p’.
