Find the value of ‘k’ if (x – 2) is a factor of x³ + 2x² – kx + 10.

Hence determine whether (x + 5) is also a factor.

If A = $\left[\begin{array}{cc}3& 5\\ 4& - 2\end{array}\right]$ and B = $\left[\begin{array}{c}2\\ 4\end{array}\right]$, is the product AB possible? Give a reason. If yes, find AB.

Mr. Kumar borrowed Rs. 15000 for two years. The rates of interest for two successive years are 8% and 10% respectively. If he repays Rs. 6200 at the end of first year, find the outstanding amount at the end of second year.

From a pack of 52 playing cards all cards whose numbers are multiples of 3 are removed. A card is now drawn at random.
(i) a face card (King, Jack or Queen) (ii) an even numbered red card

Solve the following equation:

$\mathrm{x} - \frac{18}{\mathrm{x}} = 6$. Give your answer correct to two significant figures.

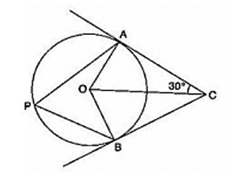
In the given figure O is the centre of the circle. Tangents A and B meet at C. If $\angle$ACO = 30$°$, find

(i) $\angle$BCO (ii) $\angle$AOB (iii) $\angle$APB

7.

Ahmed has a recurring deposit account in a bank. He deposits Rs. 2,500 per month for 2 years. If he gets Rs. 66,250 at the time of maturity, find

(i) The interest paid by the bank

(ii) The rate of interest

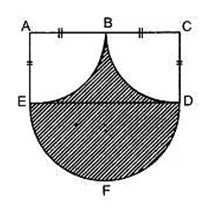
Calculate the area of the shaded region, if the diameter of the semi circle is equal to 14 cm.
Take $\mathrm{\pi } = \frac{22}{7}$.

ABC is a triangle and G(4, 3) is the centroid of the triangle. If A = (1, 3), B = (4, b) and C = (a, 1), find ‘a’ and ‘b’. Find length of side BC.

Solve the following inequation and represent the solution set on the number line 2x - 5 $\le$ 5x + 4 < 11, where x $\in$ I.