 Short Answer Type
Short Answer TypeThe median of the following observation 11, 12, 14, (x - 2), (x + 4), (x + 9), 32, 38, 47 arranged in ascending order is 24.
Find the value of x and hence find the mean.
If (x – 2) is a factor of the expression 2x3 + ax2 + bx – 14 and when the expression is divided by (x – 3), it leaves a remainder 52, find the values of a and b.
Draw a histogram from the following frequency distribution and find the mode from the graph:
| Class | 0 - 5 | 5 - 10 | 10 - 15 | 15 - 20 | 20 -25 | 25 - 30 |
| Frequency | 2 | 5 | 18 | 14 | 8 | 5 |
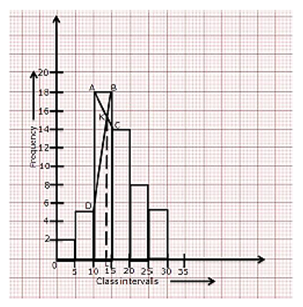
Steps to calculate mode from the graph:
(i)Mark the end points of the upper corner of rectangle with maximum frequency
as A and B.
(ii) Mark the inner corner of adjacent rectangles as C and D.
(iii) Join AC and BD to intersect at K. From K, draw KL perpendicular to x-axis.
(iv) The value of L on x- axis represents the mode.
Thus, Mode = 13
In the given figure, BAD = 65, ABD = 70, BDC = 45
(i) Prove that AC is a diameter of the circle.
(ii) Find ACB
AB is a diameter of a circle with centre C = (– 2, 5). If A = (3, – 7). Find
(i) the length of radius AC
(ii) the coordinates of B.
Solve the following equation and calculate the answer correct to two decimal places:
x2 – 5x – 10 = 0.
