Solve the following inequation and write the solution set: 13x – 5 < 15x + 4 < 7x + 12, x$\in$ R Represent the solution on a real number line.

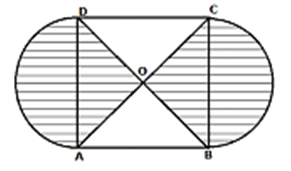
In the given figure, ABCD is a square of side 21 cm. AC and BD are two diagonals of the square. Two semicircles are drawn with AD and BC as diameters. Find the area of the shaded region. (Take $\mathrm{\pi } = \frac{22}{7}$)

The marks obtained by 30 students in a class assignment of 5 marks are given below.

Marks	0	1	2	3	4	5
No. of students	1	3	6	10	5	5

Calculate the mean, median and mode of the above distribution.

Virat opened a Savings Bank account in a bank on 16th April 2010. His pass book shows the following entries :

Date	Particulars	Withdrawal (Rs.)	Deposit (Rs.)	Balance (Rs.)
April 16, 2010	By cash	-	2500	2500
April 28th	By cheque	-	3000	5500
May 9th	To cheque	850	-	4650
May 15th	By cash	-	1600	6250
May 24th	To cash	1000	-	5250
June 4th	To cash	500	-	4750
June 30th	To cheque	-	2400	7150
July 3rd	By cash	-	1800	8950

Calculate the interest Virat earned at the end of 31st July, 2010 at 4% per annum interest. What sum of money will he receive if he closed the account on 1st August, 2010?

5.

If a, b, c are in continued proportion, prove that (a + b + c) (a – b + c) = a² + b² + c².

Calculate the mean of the following distribution :

Class Interval	0-10	10-20	20-30	30-40	40-50	50-60
Frequency	8	5	12	35	24	16

Prove that $\frac{\sin \left(\mathrm{\theta }\right)}{1 - \cot \left(\mathrm{\theta }\right)} + \frac{\cos \left(\mathrm{\theta }\right)}{1 - \tan \left(\mathrm{\theta }\right)} = \cos \left(\mathrm{\theta }\right) + \sin \left(\mathrm{\theta }\right)$

AB and CD are two chords of a circle intersecting at P. Prove that .

A bag contains 5 white balls, 6 red balls and 9 green balls. A ball is drawn at random from the bag. Find the probability that the ball drawn is:

(i) a green ball

(ii) a white or a red ball

(iii) is neither a green ball nor a white ball.

Rohit invested Rs. 9,600 on Rs. 100 shares at Rs. 20 premium paying 8% dividend. Rohit sold the shares when the price rose to Rs. 160. He invested the proceeds (excluding dividend) in 10% Rs. 50 shares at Rs. 40. Find the:

(i) original number of shares

(ii) sale proceeds

(iii) new number of shares.

(iv) change in the two dividends.