 Short Answer Type
Short Answer TypeSolve the following system of linear equation using matrix method.
3x + y + z = 1, 2x + 2z = 0, 5x + y + 2z = 2.
Verify the conditions of Rolle's Theorem for the following function.
Find a point in the interval, where the tangent to the curve is parallel to x - axis.
Find the equation of the standard ellipse, taking its axes as the coordinate axes, whose minor axis is equal to the distance between the foci and whose legth of latus rectum is 10. Also, find its eccentricity.
A rectangle is inscribed in semicircle of ardius r with one of its sides on the diameter of the semicircle. Find the dimensions of the rectangle to get maximum area. Also, find the maximum area.
Let PQRS be the rectangle inscribed in the semi-circle of radius so that OR = r, where O is in centre of circle.
Let PO = OQ = x and QR = y so that sides of rectangle are of lengths 2x and 2y respectively.
Let
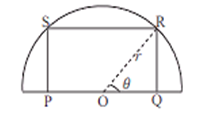
In ,
Let A be area of rectangle PQRS
= 2 OQ QR
=
= 0
is critical point.
< 0
Area is maximum at =
So, sides of rectangle are
And, Area = = r2 sq. units.
