Solution of the equation  is :

• x + y = a

• x² + y² = a²

• $\sqrt{\mathrm{x}} + \sqrt{\mathrm{y}} = \sqrt{\mathrm{a}}$

A bag contains 5 white and 3 black balls and 4 balls are successively drawn out and not replaced. The probability that they are alternately of different colours, is :

• 1/196

• 2/7

• 1/7

• 13/56

$\int {\mathrm{e}}^{- \log \left(\mathrm{x}\right)}\mathrm{dx}$ is equal to :

• e^{- log(x)} + C

• - xe^{- log(x)} + C

• e^log(x) + C

• $\log \left|\mathrm{x}\right| + \mathrm{C}$

The area cut off by the latus rectum from the parabola y² = 4ax is :

• (8/3)a sq unit

• (8/3) $\sqrt{\mathrm{a}}$ sq unit

• (3/8)a² sq unit

• (8/3)a³ sq unit

The solution of differential equation (x + y )(dx - dy) = dx + dy is :

• x - y = ke^{x - y}

• x + y = ke^{x + y}

• x + y = k(x - y)

• x + y = ke^{x - y}

$\int \frac{{\mathrm{a}}^{{\displaystyle \raisebox{1ex}{$\mathrm{x}$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}}}{\sqrt{{\mathrm{a}}^{- \mathrm{x}} - {\mathrm{a}}^{\mathrm{x}}}}\mathrm{dx}$ is equal to :

• $\frac{1}{\log \left(\mathrm{a}\right)}{\sin }^{-1}\left({\mathrm{a}}^{\mathrm{x}}\right) + \mathrm{c}$

• $\frac{1}{\log \left(\mathrm{a}\right)}{\tan }^{-1}\left({\mathrm{a}}^{\mathrm{x}}\right) + \mathrm{c}$

• $2\sqrt{{\mathrm{a}}^{- \mathrm{x}} - {\mathrm{a}}^{\mathrm{x}}} + \mathrm{c}$

• $\log \left({\mathrm{a}}^{\mathrm{x}} - 1\right) + \mathrm{c}$

If g(x) = $\frac{\mathrm{f}\left(\mathrm{x}\right) - \mathrm{f}\left(- \mathrm{x}\right)}{2}$  defined over [- 3, 3], and f(x) = 2x² - 4x + 1, then ${\int }_{- 3}^3\mathrm{g}\left(\mathrm{x}\right)\mathrm{dx}$ is equal to :

• 0

• 4

• - 4

• 8

38.

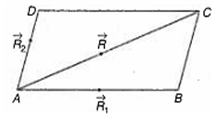
Let ABCD be the parallelogram whose sides AB and AD are represented by the vectors $2\overrightarrow{\mathrm{i}} + 4\overrightarrow{\mathrm{j}} - 5\overrightarrow{\mathrm{k}} \mathrm{and} \overrightarrow{\mathrm{i}} + 2\overrightarrow{\mathrm{j}} - 3\overrightarrow{\mathrm{k}}$ respectively. Then, if a is a unit vector parallel to $\overrightarrow{\mathrm{AC}}$, then $\overrightarrow{\mathrm{a}}$ equals:

• $\frac{1}{3}\left(3\overrightarrow{\mathrm{i}} - 6\overrightarrow{\mathrm{j}} - 2\overrightarrow{\mathrm{k}}\right)$

• $\frac{1}{3}\left(3\overrightarrow{\mathrm{i}} + 6\overrightarrow{\mathrm{j}} + 2\overrightarrow{\mathrm{k}}\right)$

• $\frac{1}{7}\left(3\overrightarrow{\mathrm{i}} - 6\overrightarrow{\mathrm{j}} - 2\overrightarrow{\mathrm{k}}\right)$

• $\frac{1}{7}\left(3\overrightarrow{\mathrm{i}} + 6\overrightarrow{\mathrm{j}} - 2\overrightarrow{\mathrm{k}}\right)$

The solution of $\frac{\mathrm{dy}}{\mathrm{dx}} + 1 = \csc \left(\mathrm{x} +\hspace{0.17em}\mathrm{y}\right)$ is  :

• $\cos \left(\mathrm{x} +\hspace{0.17em}\mathrm{y}\right) +\hspace{0.17em}\mathrm{x} = \mathrm{c}$

• $\cos \left(\mathrm{x} +\hspace{0.17em}\mathrm{y}\right) = \mathrm{c}$

• $\sin \left(\mathrm{x} +\hspace{0.17em}\mathrm{y}\right) + \mathrm{x} = \mathrm{c}$

• $\sin \left(\mathrm{x} +\hspace{0.17em}\mathrm{y}\right) + \sin \left(\mathrm{x} +\hspace{0.17em}\mathrm{y}\right) = \mathrm{c}$

Let $\overrightarrow{\mathrm{a}} \mathrm{and} \overrightarrow{\mathrm{b}}$ be two unit vectors such that angle between them is 60°. Then $\left|\overrightarrow{\mathrm{a}} - \overrightarrow{\mathrm{b}}\right|$ is equal to :

• $\sqrt{5}$

• $\sqrt{3}$

• 0

• 1