 Multiple Choice Questions
Multiple Choice QuestionsThe solution of the differential equation sec2(x)tan(y))dx + sec2(y)tan(x))dy = 0 is :
None of these
Cosine of the angle between two diagonals of a cube is equal to :
None of these
B.
Let OA, OB, OC be the sides of a cube such that OA = OB = OC = a
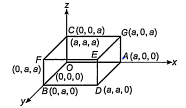
Co-ordinate of the vertices of cube are O(0, 0, 0), A(a, 0, 0), B(0, a, 0), C(0, 0, a), D(a, a, 0), E(a, a, a), F(0, a, a) and G(a, 0, a).
Direction ratios of OE are (a - 0, a - 0, a - 0) i.e., (a, a, a).
are three vectors with magnitude and such that is perpendicular to , is perpendicular to is perpendicular to . It follows that is equal to :
9
6
5
4
