The harmonic mean of two numbers is 4. Their arithmetic mean A and geometric mean G satisfy the relation 2A +G² = 27. Find the numbers.

Find the image of the point (- 8, 12) with respect to the line 4x + 7y + 13 = 0.

How many triangles can be formed by joining 6 points lying on a circle?

84.

If r² = x² + y² + z², then prove that

Determine the sum of imaginary roots of the equation (2x + x - 1) ( 4x² + 2x - 3) = 6

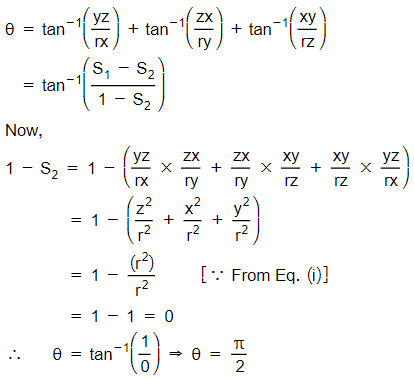
If cos(A) + cos(B) + cos(C) = 0, prove that
cos(3A) + cos(3B) + cos(3C) = 12 cos(A) cos(B)cos(C)

If the area of a rectangle is 64 sq unit, find the minimum value possible for its perimeter

Let IR be the set of real numbers and f : IR ➔ IR be such that for all x, y ∈ IR, . Prove that f is a constant function.

Find the general solution of (x + log(y))dy + ydx = 0

Prove that