Multiple Choice QuestionsThe population p(t) at time t of a certain mouse species satisfies the differential equation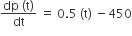 
. if p (0) = 850, then the  time at which the population becomes zero is
2 log 18
log 9
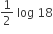
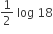
Let a, b ∈ R be such that the function f given by f(x) = ln |x| + bx
2+ ax, x ≠0 has extreme values at x = –1 and x = 2.
Statement 1: f has local maximum at x = –1 and at x = 2.
Statement 2:Â 
Statement 1 is false, statement 2 is true
Statement 1 is true, statement 2 is true; statement 2 is a correct explanation for statement 1
Statement 1 is true, statement 2 is true; statement 2 is not a correct explanation for statement 1
Statement 1 is true, statement 2 is true; statement 2 is not a correct explanation for statement 1
If: R →R is a function defined by 
 where [x] denotes the greatest integer function, then f is
continuous for every real x
discontinous only at x = 0
discontinuous only at non-zero integral values of x
discontinuous only at non-zero integral values of x
Let P and Q be 3 × 3 matrices with P ≠Q. If P3= Q3 and P2Q = Q2P, then determinant of(P2+ Q2) is equal to
-2
1
0
0
Consider the function f(x) = |x – 2| + |x – 5|, x ∈ R.
Statement 1: f′(4) = 0
Statement 2: f is continuous in [2, 5], differentiable in (2, 5) and f(2) = f(5).
Statement 1 is false, statement 2 is true
Statement 1 is true, statement 2 is true; statement 2 is a correct explanation for statement 1
Statement 1 is true, statement 2 is true; statement 2 is not a correct explanation for statement 1
Statement 1 is true, statement 2 is true; statement 2 is not a correct explanation for statement 1
Let 
 be  two unit vectors. If the vectors 
 and 
 are perpendicular to each other, then the angle between 
 isÂ
Ï€/6
Ï€/2
Ï€/3
Ï€/3
If the integral 
 then an equal toÂ
-1
-2
1
1
D.
1
| ⇒ |
Assuming the balls to be identical except for difference in colours, the number of ways in which one or more balls can be selected from 10 white, 9 green and 7 black balls is
880
629
630
630
Let ABCD be a parallelogram such that 
 and ∠BAD be an acute angle. If 
 is the vector that coincides with the altitude directed from the vertex B the side AD, then 
 is given byLet ABCD be a parallelogram such that AB = q,AD = p and ∠BAD be an acute angle. If r is the vector that coincides with the altitude directed from the vertex B to the side AD, then r is given by (1)
Switch
 then g(x +π) equals
