The value of the integral ${\int }_{\raisebox{1ex}{$\mathrm{\pi }$}\!\left/ \!\raisebox{-1ex}{$6$}\right.}^{\raisebox{1ex}{$\mathrm{\pi }$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}\left(\frac{1 +\hspace{0.17em}\sin \left(2\mathrm{x}\right) + \cos \left(2\mathrm{x}\right)}{\sin \left(\mathrm{x}\right) + \cos \left(\mathrm{x}\right)}\right)d\mathrm{x}$ is equal to

• 16

• 8

• 4

• 1

The value of the integral ${\int }_0^{\raisebox{1ex}{$\mathrm{\pi }$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}\frac{1}{1 +\hspace{0.17em}{\left(\tan \left(\mathrm{x}\right)\right)}^{101}}d\mathrm{x}$ is equal to

• 1

• $\frac{\mathrm{\pi }}{6}$

• $\frac{\mathrm{\pi }}{8}$

• $\frac{\mathrm{\pi }}{4}$

The integrating factor of the differential equation

$3{\mathrm{xlog}}_{\mathrm{e}}\left(\mathrm{x}\right)\frac{d\mathrm{y}}{d\mathrm{x}} + \mathrm{y} = 2{\log }_{\mathrm{e}}\left(\mathrm{x}\right)$ is given by

• ${\left({\log }_{\mathrm{e}}\left(\mathrm{x}\right)\right)}^3$

• ${\log }_{\mathrm{e}}\left({\log }_{\mathrm{e}}\left(\mathrm{x}\right)\right)$

• ${\log }_{\mathrm{e}}\left(\mathrm{x}\right)$

• ${\left({\log }_{\mathrm{e}}\left(\mathrm{x}\right)\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$3$}\right.}$

The value of the integral ${\int }_0^{\raisebox{1ex}{$\mathrm{\pi }$}\!\left/ \!\raisebox{-1ex}{$4$}\right.}\frac{\sin \left(\mathrm{x}\right) + \cos \left(\mathrm{x}\right)}{3 + \sin \left(2\mathrm{x}\right)}d\mathrm{x}$ is equal to

• ${\log }_{\mathrm{e}}\left(2\right)$

• ${\log }_{\mathrm{e}}\left(3\right)$

• $\frac{1}{4}{\log }_{\mathrm{e}}\left(2\right)$

• $\frac{1}{4}{\log }_{\mathrm{e}}\left(3\right)$

The value of the integral ${\int }_{- 2}^2\left(1 + 2\sin \left(\mathrm{x}\right)\right){\mathrm{e}}^{\left|\mathrm{x}\right|}d\mathrm{x}$ is equal to

• 0

• e² - 1

• 2(e² - 1)

• 1

76.

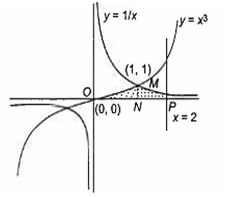
The area of the region bounded by the curves y = x , y = $\frac{1}{\mathrm{x}}$, x = 2 is

• 4 - ${\log }_{\mathrm{e}}\left(2\right)$

• $\frac{1}{4} + {\log }_{\mathrm{e}}\left(2\right)$

• $3 - {\log }_{\mathrm{e}}\left(2\right)$

• $\frac{15}{4} - {\log }_{\mathrm{e}}\left(2\right)$

Let y be the solution of the differential equation

$\mathrm{x}\frac{d\mathrm{y}}{d\mathrm{x}} = \frac{{\mathrm{y}}^2}{1 - \mathrm{ylog}\left(\mathrm{x}\right)}$ satisfying y(1) = 1. Then, y satisfies

• y = x^{y - 1}

• y = x^y

• y = x^{y + 1}

• y = x^{y + 2}

The area of the region, bounded by the curves y = sin- ¹(x) + x(1 - x) and y = sin^{- 1} (x) - x(1 - x) in the first quadrant, is

• 1

• $\frac{1}{2}$

• $\frac{1}{3}$

• $\frac{1}{4}$

The value of the integral ${\int }_1^5\left[\left|\mathrm{x} - 3\right| + \left|1 - \mathrm{x}\right|\right]d\mathrm{x}$ is equal to

• 4

• 8

• 12

• 16

Let [x] denote the greatest integer less than or equal to x, then the value of the integral ${\int }_{- 1}^1\left(\left|\mathrm{x}\right| - 2\left[\mathrm{x}\right]\right)d\mathrm{x}$ is equal to

• 3

• 2

• - 2

• - 3