 Multiple Choice Questions
Multiple Choice QuestionsThe vector equation of the plane through the point (2, 1, - 1) and parallel to the plane r - (i + 3j - k) = 0 is
r . (i + 9j + 11k) = 6
r . (i - 9j + 11k) = 4
r . (i + 3j - k) = 6
r . (i + 3j - k) = 4
If the foot of the perpendicular drawn from the point (5, 1, - 3) to a plane is (1, - 1, 3), then the equation of the plane is
2x + y - 3z + 8 = 0
2x + y + 3z + 8 = 0
2x - y - 3z + 8 = 0
2x - y + 3z + 8 = 0
A.
2x + y - 3z + 8 = 0
Let equation of a plane passing through (1, - 1, 3) is
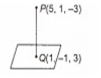
a(x - 1) + b(y + 1) + c(z - 3) = 0
Now, DR's of PQ = (5 - 1, 1 + 1, - 3- 3)
= (4, 2, - 6)
The normal to the plane are proportional to PQ.
i.e., (a, b, c) = (4, 2, - 6) or (2, 1, - 3)
2(x - 1) + 1(y + 1) - 3(z - 3) = 0
2x + y - 3z + 8 = 0
The equation of the plane through the line of intersection of the planes x - y + z + 3 = 0 and x + y + 22 + 1 = 0 and parallel to x-axis is
2y - z = 2
2y + z = 2
4y + z = 4
y - 2z = 3
