 Multiple Choice Questions
Multiple Choice QuestionsThe values of x, y and z for the system of equations x + 2y + 3z = 6, 3x - 2y + z = 2 and 4x + 2y + z = 7 are respectively
1, 1, 1
1, 2, 3
1, 3, 2
2, 3, 1
The relation R in R defined by R = {(a, b): a b3), is
reflexive
symmetric
transitive
None of these
Let f (x + y) = f(x) + f(y) for all x and y. If the function f(x) is continuous at x = 0, then f(x) is continuous
only at x = 0
for all x
None of these
The altitude of the right circular cone of maximum volume that can be inscribed in a sphere of radius r is
Let f(x) = x(x - 1)2, the point at which f(x) assumes maximum and minimum are respectively
3, 1
None of these
Rectangles are inscribed ina circle of radius r. The dimensions of the rectangle which has the maximum area, are
r, r
2r, 2r
None of the above
C.
Let ABCD be the rectangle inscribed in a circle of radius r.
Let AB = x
and BC = y
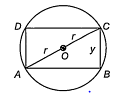
Then, x2 + y2 = 4r2
