Let $\square$PQRS be a quadrilateral. If M and N are the mid-points of the sides PQ and RS respectively, then PS + QR =

• 3 MN

• 4 MN

• 2 MN

• 2 NM

If vector r with dc's l, m, n is equally inclined to the coordinate axes, then the total number of such vectors is

• 4

• 6

• 8

• 2

$\int \frac{1}{\left({\mathrm{x}}^2 + 4\right)\left({\mathrm{x}}^2 + 9\right)}\mathrm{dx} = {\mathrm{Atan}}^{-1}\left(\frac{\mathrm{x}}{2}\right) + {\mathrm{Btan}}^{-1}\left(\frac{\mathrm{x}}{3}\right) + \mathrm{C}$, then A - B =

• $\frac{1}{6}$

• $\frac{1}{30}$

• $- \frac{1}{30}$

• $- \frac{1}{6}$

If $\sqrt{\frac{\mathrm{x} - 5}{\mathrm{x} - 7}}\mathrm{dx} = \mathrm{A}\sqrt{{\mathrm{x}}^2 - 12\mathrm{x} +\hspace{0.17em}35}$ + $\log \left|\mathrm{x} - 6 + \sqrt{{\mathrm{x}}^2 - 12\mathrm{x} + 35}\right| + \mathrm{C}$, then A =

• - 1

• $\frac{1}{2}$

• $- \frac{1}{2}$

• 1

At random variable X $~$ B(n, p), if values of mean and variance of X are 18 and 12 respectively, then total number of possible values of X are

• 54

• 55

• 12

• 18

The area of the region bounded by the lines y = 2x + 1, y = 3x + 1and x = 4 is

• 16 sq unit

• $\frac{121}{3} \mathrm{sq} \mathrm{unit}$

• $\frac{121}{6} \mathrm{sq} \mathrm{unit}$

• 8 sq unit

27.

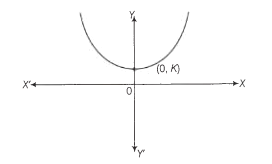
The differential equation of all parabolas whose axis is Y-axis, is

• $\mathrm{x}\frac{{\mathrm{d}}^2\mathrm{y}}{{\mathrm{dx}}^2} - \frac{\mathrm{dy}}{\mathrm{dx}} = 0$

• $\mathrm{x}\frac{{\mathrm{d}}^2\mathrm{y}}{{\mathrm{dx}}^2} + \frac{\mathrm{dy}}{\mathrm{dx}} = 0$

• $\frac{{\mathrm{d}}^2\mathrm{y}}{{\mathrm{dx}}^2} - \mathrm{y} = 0$

• $\frac{{\mathrm{d}}^2\mathrm{y}}{{\mathrm{dx}}^2} - \frac{\mathrm{dy}}{\mathrm{dx}} = 0$

${\int }_0^3\left[\mathrm{x}\right]\mathrm{dx} = ...,$ where [x] is greatest integer function

• 3

• 0

• 2

• 1

The objective function of LPP defined over the convex set attains it optimum value at

• atleast two of the corner points

• all the corner points

• atleast one of the corner points

• None of the corner points

The equation of the plane through (- 1, 1, 2) whose normal makes equal acute angles with coordinate axes is

• $\mathrm{r}. \left(\hat{\mathrm{i}} + \hat{\mathrm{j}} + \hat{\mathrm{k}}\right) = 2$

• $\mathrm{r}. \left(\hat{\mathrm{i}} + \hat{\mathrm{j}} + \hat{\mathrm{k}}\right) = 6$

• $\mathrm{r}. \left(3\hat{\mathrm{i}} - 3\hat{\mathrm{j}} + 3\hat{\mathrm{k}}\right) = 2$

• $\mathrm{r}. \left(\hat{\mathrm{i}} - \hat{\mathrm{j}} + \hat{\mathrm{k}}\right) = 3$