 Multiple Choice Questions
Multiple Choice QuestionsOne solid sphere A and another hollow sphere B are of same mass and same outer radii. Their moment of inertia about their diameters are respectively IA and IB such that
Where dA and dB are their densities.
IA = IB
IA > IB
IA < IB
IA < IB
Spherical balls of radius R are falling in a viscous fluid of viscosity η with a velocity v. The retarding viscous force acting on the spherical ball is
directly proportional to R but inversely proportional to v.
directly proportional to both radius R and velocity v.
inversely proportional to both radius R and velocity v.
inversely proportional to both radius R and velocity v.
If two soap bubbles of different radii are connected by a tube,
air flows from the bigger bubble to the smaller bubble till the sizes are interchanged.
air flows from bigger bubble to the smaller bubble till the sizes are interchanged
air flows from the smaller bubble to the bigger.
air flows from the smaller bubble to the bigger.
The bob of a simple pendulum executes simple harmonic motion in water with a period t, while the period of oscillation of the bob is t0 in the air. Neglecting frictional force of water and given that the density of the bob is (4/3) x 1000 ms-1 . What relationship between t and t0 is true?
t = t0
t = t0/2
t = 2t0
t = 2t0
A particle at the end of a spring executes simple harmonic motion with a period t1, while the corresponding period for another spring is t2. If the period of oscillation with the two springs in series is t, then
T = t1 + t2



The total energy of particle, executing simple harmonic motion is
∝ x
∝ x2
independent of x
independent of x
The displacement y of a particle in a medium can be expressed as y = 10−6 sin(110t + 20 x + π/4) m, where t is in seconds and x in a meter. The speed of the wave is
2000 m/s
5 m/s
20 m/s
20 m/s
A particle of mass m is attached to a spring (of spring constant k) and has a natural angular frequency ω0. An external force F(t) proportional to cosωt (ω≠ω0) is applied to the oscillator. The time displacement of the oscillator will be proportional to
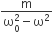
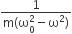
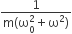
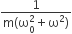
B.
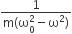
Initial angular velocity of particle = ω0 and at any instant t, angular velocity = ω Therefore, for a displacement x, the resultant acceleration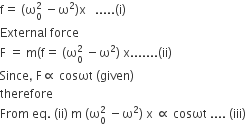
Now, equation of simple harmonic motion
x = A sin (ωt + φ) .......... (iv)
at t = 0 ; x = A
∴ A = A sin( 0 + φ )
⇒ φ =π/2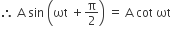 ..........(v)
..........(v)
Hence, from equations (iii) and (v), we finally get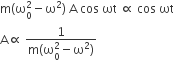
In forced oscillation of a particle the amplitude is maximum for a frequency ω1 of the force, while the energy is maximum for a frequency ω2 of the force, then
ω1 = ω2
ω1 > ω2
ω1 < ω2 when damping is small and ω1 > ω2 when damping is large
ω1 < ω2 when damping is small and ω1 > ω2 when damping is large
