 Multiple Choice Questions
Multiple Choice QuestionsWhat is the number of ways in which the letters of the word ‘ABLE’ can be arranged So that the Vowels occupy even places ?
2
4
6
8
B.
4
Consider word : ABLE
Vowels : A , E
Consonants : B, L
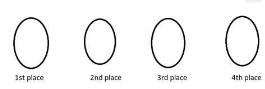
If vowels can take only even place then first fix vowels at even places.
Then consonants can be arranged in two ways :
| 1st place | 3rd place |
| B | L |
| L | B |
Also , these vowels can also be arranged in two ways.
Hence, Required Number of ways = 2 X 2 = 4
Let S = {1, 2, 3, ...}. A relation R on S × S is defined by x Ry if loga(x) > loga(y) when , Then the relation is
reflexive only
symmetric only
transitive only
both symmetric and transitive
If 1.5 ≤ x ≤ 4.5, then which one of the following is correct ?
(2x – 3) (2x – 9) > 0
(2x – 3) (2x – 9) < 0
(2x – 3) (2x – 9) ≥ 0
(2x – 3) (2x – 9) ≤ 0
If, x = logc (ab), y = loga(bc), z = logb(ca), then which of the following is correct ?
xyz = 1
x + y + z = 1
(1 + x)-1 + (1 + y)-1 + (1 + z)-1 = 1
(1 + x)-2 + (1 + y)-2 + (1 + z)-2 = 1
The number (1101101 + 1011011)2 can be written in decimal system as
(198)10
(199)10
(200)10
(201)10
