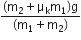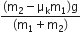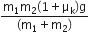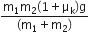If energy (E), velocity (v) and time (T) are chosen  as the fundamental quantities, the dimensional formula of surface tension will be

• [Ev^-2T^-1]

• [Ev^-1T^-2]

• [Ev^-2T^-2]

• [Ev^-2T^-2]

A particle of unit mass undergoes one-dimensional motion such that its velocity according to
V(x) =  βx^-2n where β and n are constants and x is the position of the particle. The acceleration of the particle as a function of x is given by 

• -2nβ² x^-2n-1

• -2nβ² x^-4n-1

• -2β x^-2n+1
  

• -2β x^-2n+1
  

Two similar springs P and Q have spring constants K_P and KQ, such that K_P>K_Q. They are stretched, first by the same amount (case a), then by the same force (case b). The work done by the springs W_P and W_Q are related as, in  case (a) and case (b), respectively

• W_P =W_Q ;W_P> W_Q

• W_P =W_Q ;W_P= W_Q

• W_P > W_Q ;W_Q> W_P

• W_P > W_Q ;W_Q> W_P

4.

A block of mass 10 kg, moving in the x-direction with a constant speed of 10 ms^-1 , is subjected to a retarding force F= 0.1x J/m during its travel from x = 20 m to 30 m. Its final KE will be

• 475 J

• 450 J

• 275 J

• 275 J

A particle of mass m is driven by a machine that delivers a constant power K watts. If the particle starts from rest, the force on the particle at time t is

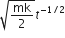
Two particles of masses m₁,m₂ move with initial velocities u₁ and u₂. On collision, one of the particles gets excited to a higher level, after absorbing energy (E). If final velocities of particles be v₁ and v₂, then we must have

Kepler's third law states that square of the period of revolution (T) of a planet around the sun, is proportional to the third power of average distance r between the sun and planet i.e, T² =Kr³, here K is constant.
If  the masses of the sun and planet are M and m respectively, them as per Newton's law of gravitation force of attraction between them is 


The relation between G and K is described as

• GK =4π²

• GMK =4π²

• K=G

• K=G

A ship A is moving Westwards with a speed of 10 kmh^-1 and a ship B 100km  south of A, is moving Northwards with a speed of 10 kmh^-1. The time after which the distance between them becomes shortest is

• 0 h

• 5 h

• 
• 

Three blocks A, B, and C of masses 4 kg, 2 kg and 1 kg respectively, are in contact on a 14 N is applied to the 4 kg block, then the contact force between A and B is

• 2 N

• 6 N

• 8 N 

• 8 N 

A block A of mass m₁ rests on a horizontal table. A light string connected to it passes over a frictionless pulley at the edge of the table and from its other end, another block B of mass m₂ is suspended. The coefficient of kinetic friction between the block and the table is . When the block A is sliding on the table, the tension in the string is