If  equals to

• 

• 

• 1

• 3

O is an centre of a circle. P is an external point of it at distance of 13 cm from O. The radius of the circle is 5 cm. Then the length of a tangent to the circle P upto the point of contact is

• √194 cm

• 10 cm

• 12 cm

• 8 cm

If θ is acute angle and sin (θ + 18°) = 1/2, then the value of θ in circular measure is:

64.

18 men or 36 boys working 6 hours a day can plough a field in 24 days. In how many days will 24 men and 24 boys working 9 hours a day plough the same field?

• 9

• 10

• 6

• 8

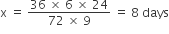
If a(x + y) =  b(x - y)  = 2ab, the the value of 2(x² + y²) is

• 2 (a² - b²)

• 2(a² + b²)

• 4(a² - b²)

• 4(a² + b²)

If  then the value of  is:

• 23

• 16

• 34

• 32

G is the centroid of the equilateral Δ ABC, if AB = 9 cm, then AG is equal to:

• 

• 3 cm

• 

• 6 cm

In the figure (not drawn to scale) given below, if AD = DC = BC and , then  then  is

• 32°

• 84°

• 64°

• 96°

If θ is positive acute angle and 4 sin²θ = 3, then the value of  is

• 1

• 0

• 

• 

The chord AB of a circle of centre O subtends an angle θ with the tangent at A to the circle. Then measure of 

• θ

• 90° - θ

• 90° + θ

• 2 (180° - θ)