Prove that  is irrational.

Let us assume that  is rational.

We know that rational number can be written as  where ‘a’ and ‘b’ are integers and b ≠ 0.
i.e., assume that



Squaring both side, we get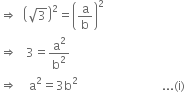

⇒ a² is divisible by 3

⇒ a is divisible by 3

Let a = 3c for some integer ‘c’.

Putting a = 3c in (i)

a² = 3b²

⇒    (3c)² = 3b²

⇒    9c² = 3b²

⇒    b² = 3c²

⇒ b² is divisible by

⇒ b is divisible by 3

Thus, 3 is a common factor of ‘a’ and ‘b’.

But this contradicts the fact that ‘a’ and ‘b’ have no common factor other than 1.
The contradiction arises by assuming that  is rational.
Hence,    is irrational.