Represent the following situation in the form of a quadratic equation:
The hypotenuse of a right-angled triangle is 20 meters. If the difference between the lengths of the other sides be 4 meters.

Let one side (AB) = (x – 4)m
Other side (BC) = x m
and hypotenuse = 20 m
We know,
AC² = AB² + BC²
⇒ (20)² = (x – 4)² + (x)²
⇒ 400 = x² + 16 – 8x + x²
⇒ 400 = 2x² – 8x + 16
⇒ 2x² – 8x – 384 = 0
⇒ 2(x² – 4x –192) = 0
⇒ x²– 4x – 192= 0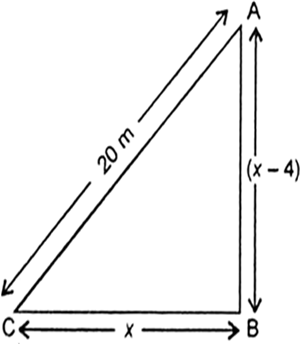

Therefore, the required representation in the form of quadratic equation be x²– 4x –192 = 0.